مدارات محاسبه کننده آنالوگ؛ قسمت سوم

باید هشدار داد که استفاده از تکنیک های حسابان برای استخراج یک کمیت از کمیت دیگر محدودیتهای خاص خود را دارد. مشتق گیری تمایل نامطلوبی برای تقویت "نویز" موجود در متغیر اندازه گیری شده دارد، چرا که نویز معمولاً با فرکانس هایی بسیار بیشتر از فرکانس متغیر اندازه گیری شده ظاهر می شود و فرکانس های بالاتر به دلیل ماهیت خود دارای نرخ تغییر بالاتری در طول زمان هستند. 

برای نشان دادن این مشکل، فرض کنید که ما از سیگنال سرعت به دست آمده از یک تاکوژناتور ذغالی، برای اندازه گیری شتاب یک خودرو استفاده کنیم. اتصال ضعیف ذغالها یک سری افتهای لحظه ای در ولتاژ خروجی تاکوژنراتور ایجاد می کنند و مشتق گیر متصل به آن، این افتها را به عنوان تغییرات بسیار سریع سرعت تفسیر می کند. برای خودرویی که با سرعت ثابت حرکت می کند، و نه شتاب افزاینده یا کاهنده دارد، سیگنال شتاب باید 0 ولت باشد ، اما "نویز" ناشی از یک تاکوژنراتور معیوب باعث می شود در سیگنال مشتق گیری شده دارای نیزه هایی باشیم که به صورت اشتباه دوره های کوتاه افزایش یا کاهش سرعت را نشان می دهد. 

لازم نیست که دامنه ولتاژ نویز موجود در سیگنال مشتق گیری شده خیلی زیاد باشد تا مشکل ایجاد کند. تنها چیزی که لازم است این است که شکل موج نویز افزایش یا کاهش سریعی داشته باشد. به عبارت دیگر، هر نویز الکتریکی با مؤلفه dv/dt زیاد هنگام مشتق گیری مشکل ساز خواهدشد حتی اگر دامنه کمی داشته باشد. 

لازم به ذکر است که مشکل خطای ویژه مدارهای اندازه گیری/محاسباتی ناشی از طبیعت مدارات آنالوگ نیست، بلکه بیشتر ناشی از ذات فرآیند مشتق گیری است. مهم نیست که چگونه مشتق گیری کنیم، "نویز" در سیگنال سرعت همواره سیگنال خروجی را خراب می کند. مطمئناً، اگر از یک سیگنال دو بار مشتق بگیریم، همانطور که برای دستیابی به سرعت و شتاب از سیگنال موقعیت عمل کردیم، نویز تقویت شده توسط مدار مشتق گیر اول دوباره توسط مشتق گیر بعدی تقویت می شود، بنابراین دارای یک مسئله ی ترکیبی می شویم. 

انتگرال گیری چنین مشکلی ندارد، زیرا انتگرال گیرها همانند یک فیلتر پایین گذر عمل می کنند و سیگنال های ورودی با فرکانس بالا را کاهش می دهند. در واقع ، تمام قله های بالا و پایین ناشی از نویز سیگنال با گذشت زمان همدیگر را خنثی می کنند تا نتیجه حاصل کاهش یابد. بنابراین ممکن است تصور شود که ما می توانیم با اندازه گیری مستقیم شتاب و انتگرال گیری از آن برای بدست آوردن سرعت، از این مشکلات پرهیز کنیم. در واقع، محاسبه را به صورت "معکوس" روشی که قبلا نشان داده شد پیش ببریم. 

متأسفانه، پیروی از این روش ممکن است ما را به سوی مشکلات دیگری سوق دهد، که یکی از آنها اشکالی رایج در انتگرال گیرهای آنالوگ معروف به رانش (drift) است. همه تقویت کننده های عملیاتی مقداری جریان بایاس ورودی دارند و این جریان تمایل دارد تا به همراه بار ناشی از سیگنال ولتاژ ورودی در خازن ذخیره شود. به عبارت دیگر، انتگرال گیرهای آنالوگ از گرایش ولتاژ خروجی شان به سوی رانش رنج می برند حتی اگر هیچ ولتاژی در ورودی نداشته باشند و در نتیجه در طول زمان دارای یک خطای تجمعی هستند. البته خازن های غیر ایده آل به دلیل مقاومت داخلی تمایل دارند تا بار ذخیره شده در خود را با گذشت زمان از دست بدهند و در نتیجه جابجایی ولتاژ خروجی به سمت صفر می رود. این مشکلات ناشی از طبیعت مدارهای آنالوگ است و ممکن است با استفاده از مدارات محاسباتی دیجیتال برطرف شوند. 

با وجود اشکالات مداری، خطاهای احتمالی ممکن است ناشی از انتگرال گیری یک کمیت (مانند شتاب) برای بدست آوردن کمیت دیگر (مانند سرعت) باشد، چرا که انتگرال گیرهای این گونه کار می کنند. اگر نقطه "صفر" سنسور سیگنال اولیه به صورت ایده آل کالیبره نباشد، حتی در شرایطی که خروجی وجود ندارد، یک سیگنال مثبت یا منفی جزئی تولید می کند. خودروی را در نظر بگیرید که دارای شتاب سنج کالیبره نشده ای غیر ایده آل است، یا شتاب سنجی که تحت تأثیر جاذبه شتاب کمی را بدون وجود شتاب خودرو تشخیص می دهد. حتی با وجود یک انتگرال گیر ایده آل، این خطای حسگر باعث خطای تجمعی در انتگرال گیر می شود، در نتیجه سیگنال خروجی نشانگر تغییر سرعت است در حالی که خودرو نه شتاب می گیرد و نه کند می شود. 

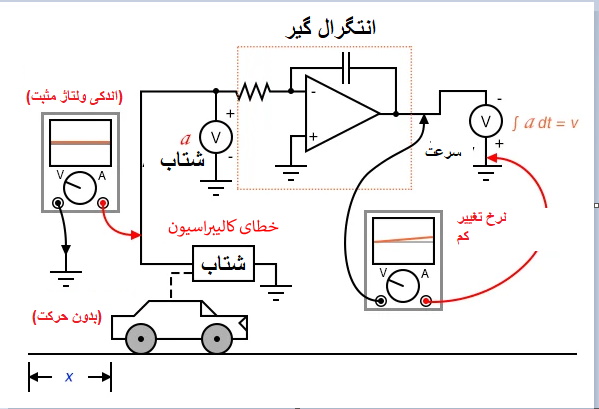
همانند فرایند مشتق گیری، اگر سیگنال انتگرال گیری شده به انتگرال دیگری تغذیه شود، این خطا نیز مرکب خواهد شد زیرا خروجی جابجا شده اولین انتگرال گیر به زودی سیگنال مثبت یا منفی قابل توجهی را برای انتگرال گیر بعدی ایجاد می کند. بنابراین، هنگام انتگرال گیری از سیگنال های حسگر باید دقت شود: اگر سنسور کاملا بر روی "صفر" تنظیم نشده نباشد، خروجی انتگرال گیر جابجا می شود حتی اگر خود انتگرال گیر ایده آل باشد. 

تا کنون، تنها خطاهای انتگرال گیری ناشی از طبیعت مدارها مورد بحث بوده اند: خطاهای ناشی از ایده آل نبودن مدارها و حسگرها. همچنین یک منبع خطای ذاتی ناشی از خود روند انتگرال گیری هم وجود دارد و آن مسئله ثابت ناشناخته است. کسانی که در حساب انتگرال مبتدی هستند نیز می دانند که هر زمان از یک تابع انتگرال گیری بشود، یک ثابت ناشناخته در معادله ظاهر می شود که معمولاً آن را با متغیر C نشان می دهند. درک این عدم قطعیت با مقایسه مشتقات چندین توابع که فقط مقدار ثابت آنها متفاوت است، قابل درک است. 

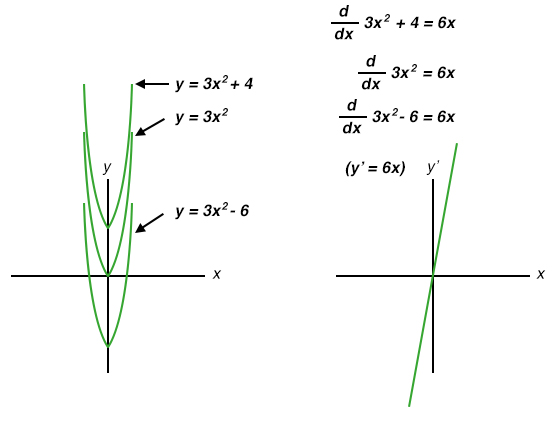
توجه داشته باشید که چگونه هر یک از این سهمی ها (y = 3x2 + C) دارای شکل مشابهی هستند که تنها در مقدار عرض از مبدأ با یکدیگر تفاوت دارند. با این حال ، همه آنها مشتق دقیقاً یکسانی دارند: y'=6x، زیرا همه آنها دارای نرخ تغییر یکسان (شیب) در مقایسه با محور x هستند. گرچه این امر از منظر مشتق گیر کاملاً طبیعی است و انتظار می رود که معادلات مختلف مشتق مشترکی داشته باشند، با این وجود  از دید انتگرال گیر عجیب به نظر می رسند، زیرا چندین پاسخ صحیح برای انتگرال یک تابع وجود دارد. مشتق گیری از یک معادله فقط یک پاسخ دارد، اما انتگرال گیری از همان مشتق برای رسیدن به معادله اصلی ما را به سمت یکسری راه حل های صحیح سوق می دهد. به افتخار این عدم اطمینان، عملکرد نمادین انتگرال گیری را انتگرال نامعین می نامند. 

هنگامی که انتگرال گیر عملیات انتگرال گیری یک سیگنال را نسبت به زمان انجام می دهد، خروجی عبارت است از مجموع سیگنالهای ورودی در طول زمان علاوه بر مقدار اولیه با دامنه دلخواه، که نشان دهنده خروجی قبلی انتگرال گیر در زمان شروع انتگرال گیری است. به عنوان مثال، اگر سرعت یک خودرو در حال حرکت در یک مسیر مستقیم را، که از شهر دور می شود، انتگرال گیری کنم، محاسبه می کنم که سرعت ثابت 50 مایل در ساعت و در مدت زمان 2 ساعت باعث طی مسافت 100 مایل (v.dt∫) می شود، و البته این بدان معنا نیست که خودرو بعد از 2 ساعت 100 مایل با شهر فاصله دارد. تنها چیزی که این نتیجه به ما می گوید این است که خودرو بعد از 2 ساعت رانندگی 100 مایل دورتر از شهر خواهد بود. فاصله واقعی از شهر پس از 2 ساعت رانندگی بستگی به فاصله ابتدایی خودرو از شهر در زمانی دارد که انتگرال گیری آغاز شده است. اگر این مقدار اولیه را برای مسافت ندانیم، پس از 2 ساعت رانندگی نمی توانیم فاصله دقیق خودرو از شهر را تعیین کنیم. 

همین مشکل وقتی ظاهر می شود که از شتاب برای به دست آوردن سرعت، نسبت به زمان، انتگرال گیری کنیم. 

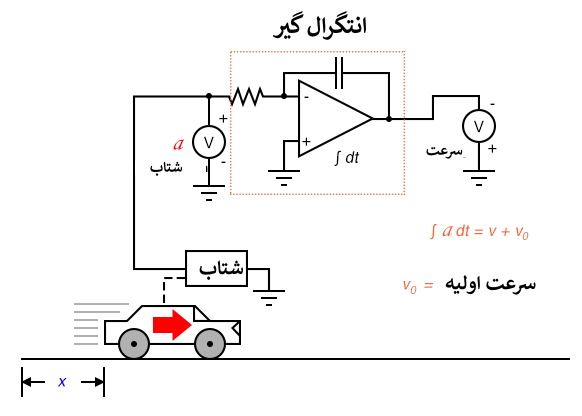
در این انتگرال گیر، سرعت محاسبه شده خودرو فقط در صورتی معتبر خواهد بود که انتگرال گیر هنگام ثابت بودن خودرو (0=v) با مقدار خروجی صفر مقداردهی اولیه شود. در غیر این صورت، انتگرال گیر می تواند هنگام توقف خودرو سیگنال غیر صفر برای سرعت (v0) نشان دهد، زیرا شتاب سنج نمی تواند تفاوت بین یک حالت توقف (0 مایل در ساعت) و یک حالت سرعت ثابت را، مثلا  60 مایل در ساعت، تشخیص دهد. این عدم قطعیت در خروجی انتگرال گیر ذاتی فرایند انتگرال گیری است، نه اینکه ناشی از مدارها یا حسگرها باشد. 

به طور خلاصه، اگر حداکثر دقت برای اندازه گیری کمیتهای فیزیکی مورد نظر است، بهتر است که آن متغیر را مستقیماً اندازه گیری کنید تا اینکه از سایر اندازه گیری ها استخراج کنید. این بدان معنا نیست که مدارات محاسب بی فایده اند. کاملاً برعکس، غالباً محاسبه تنها وسیله عملی برای به دست آوردن اندازه گیری مطلوب است. با این حال ، محدودیتهای مدارات محاسب باید درک شوند و به منظور رسیدن به اندازه گیری های دقیق مورد توجه قرار بگیرند. 

مدارات محاسبه کننده آنالوگ؛ قسمت دوم

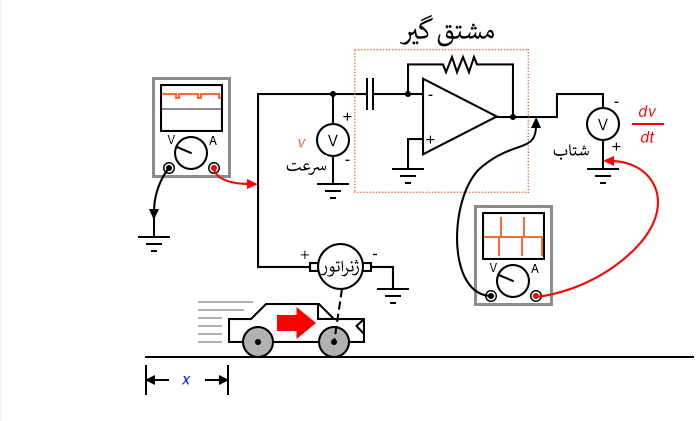
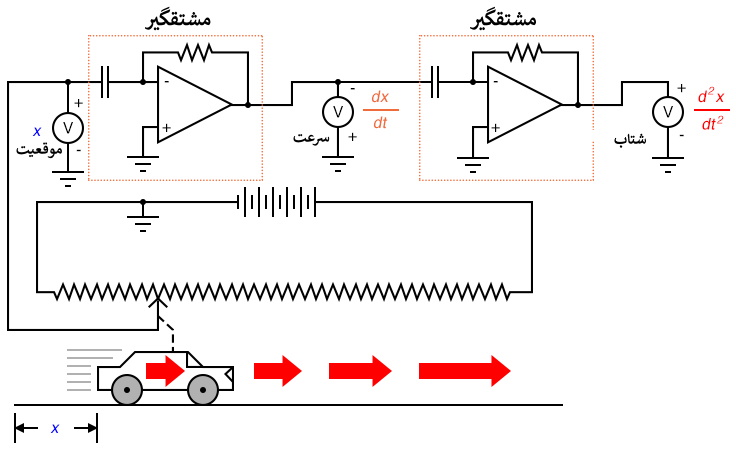
توجه داشته باشید که سرعت ثبت شده توسط ولتمتر (در خروجی مدار مشتق گیر) با قطبیت "معکوس" در خروجی تقویت کننده عملیاتی ظاهر می شود. این امر به این دلیل است که مدار مشتق گیر نشان داده شده است معکوس کننده هم هست: به ازای یک ولتاژ مثبت در ورودی، یک ولتاژ منفی به خروجی اعمال می شود. اگر بخواهیم که ولتمتر مقداری مثبت را برای سرعت نشان بدهد، باید همانطور که در تصویر نشان داده شده، به تقویت کننده عملیاتی متصل شود. اگرچه غیرممکن است که پتانسیومتر غول پیکری به متحرکی مانند یک خودرو وصل شود، این مفهوم باید روشن شده باشد که: با انجام مشتق گیری بر روی سیگنال، که نمایشگر موقعیت فعلی است، به یک سیگنال نمایشگر سرعت دست یافته ایم. 

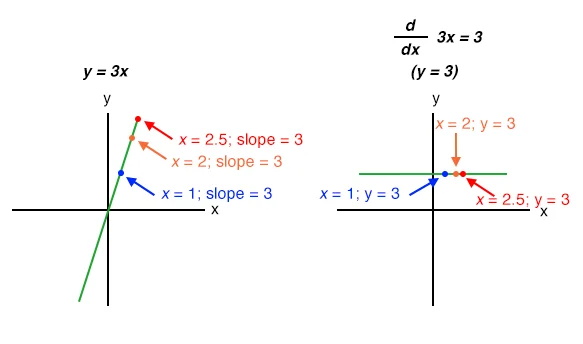
دانش آموزان در شروع فراگیری حساب دیفرانسیل روشهای ریاضی را برای مشتق گیری یاد می گیرند. با این وجود، لازم است که معادله توصیف کننده تابع اصلی شناخته شود. به عنوان مثال، دانش آموزان یاد می گیرند که چگونه مشتق یک تابع مانند y = 3x را  را به سادگی با دستکاری کردن معادله تابع پیدا کنند. می توانیم که دقت این دستکاریها را با مقایسه نمودار دو توابع بررسی کنیم: 

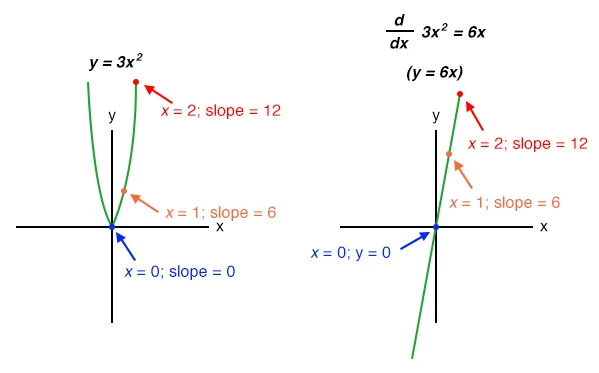
تابع غیرخطی مانند y=3x2 ممکن است که با روشهای ریاضی مشتق گیری شود. در این صورت مشتق برابر خواهد بود با 6x. 

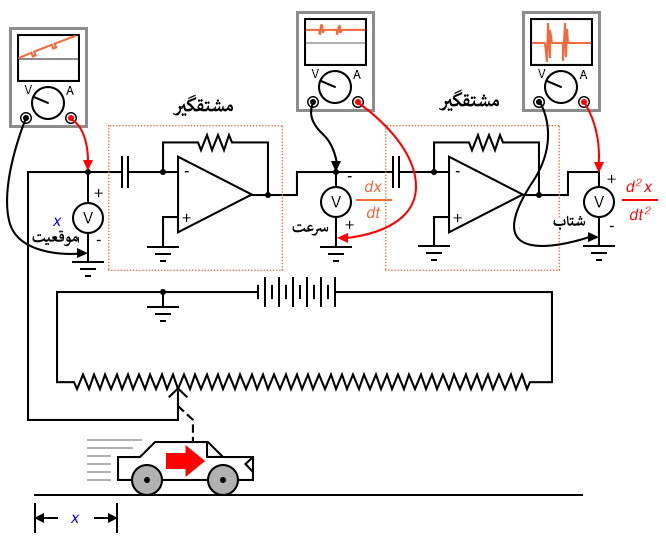
با این حال، در زندگی واقعی اغلب نمی توانیم رفتار یک رویداد فیزیکی را با یک معادله ی ساده مثل y = 3x توصیف کنیم، و بنابراین روشهای نمادین مشتق گیری دبیرستانی ممکن است برای اندازه گیری های فیزیکی غیرممکن باشد. اگر کسی بخواهد از موقعیت فرضی خودروی ما با روشهای ریاضی مشتق بگیرد(dx/dt=speed) ، ابتدا باید معادله ی موقعیت خودرو را با توجه به اندازه گیری موقعیت در یک آزمایش واقعی بدست آورد، امری که تقریبا غیرممکن است مگر اینکه خودرو تحت شرایط دقیق کنترل شده حرکت کند و منجر به ساخت یک نمودار ساده از موقعیت شود. با این حال، یک مدار مشتق گیر آنالوگ، با بهره گیری از رابطه ی خازن نسبت به ولتاژ، جریان و زمان i=C (dv/dt)، به طور طبیعی از هر سیگنال واقعی ولتاژ نسبت به زمان مشتق می گیرد، و می تواند سیگنالی متناسب با سرعت لحظه ای (dx/dt) را به دست دهد. با ترسیم سیگنال موقعیت خودرو نسبت به سیگنال خروجی مشتق گیر در یک نمودار، هر دو نمودار به طور طبیعی خود را برای تجزیه و تحلیل به نمایش می گذارند. 

می توانیم با اعمال سیگنال سرعت به یک مشتق گیر دیگر، مشتق گیری را یک گام دیگر به جلو ببریم. به عبارت دیگر، از آن برای محاسبه نرخ تغییر سرعت، که خودش نرخ تغییر موقعیت است، استفاده کنیم. برای عملی کردن این فکر چه اقدامی می توانیم انجام دهیم؟ به این امر از دید واحدهایی که برای اندازه گیری موقعیت و سرعت استفاده کردیم نگاه کنید. اگر برای تعیین موقعیت خودرو از نقطه شروع خود از مایل استفاده کنیم، احتمالا سرعت آن را با واحد مایل بر ساعت (dx/dt) بیان می کنیم. اگر از سرعت (با واحد مایل بر ساعت) نسبت به زمان مشتق بگیریم، به واحد مایل بر ساعت بر ساعت می رسیم. در فیزیک مقدماتی به دانش آموزان درباره سقوط آزاد می آموزند که اندازه گیری موقعیت با متر، سرعت با متر بر ثانیه و تغییر سرعت در طول زمان با متر بر ثانیه بر هر ثانیه انجام می شود. این آخری شتاب نامیده می شود: نرخ تغییر سرعت در واحد زمان. 

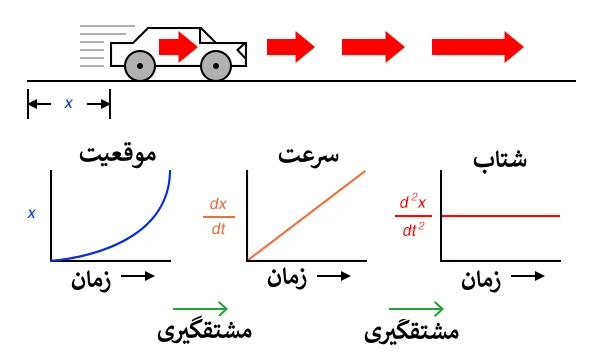
فرمول d2x/dt2 مشتق دوم موقعیت (x) نسبت به زمان (t) نامیده می شود. اگر مشتق گیر دوم را به خروجی اولی وصل کنیم، آخرین ولتمتر شتاب را ثبت می کند. 

با به دست آوردن سرعت از موقعیت و شتاب از سرعت، اصول مشتق گیری را به وضوح می توانیم ببینیم. این ها شاید که تنها اندازه گیری های فیزیکی مرتبط با هم به این روش نباشند، اما شاید که شایع ترین آنها باشند. مثال دیگری از حساب دیفرانسیل در عمل رابطه بین جریان(q)  و حجم مایع (v) انباشته شده در یک مخزن نسبت به زمان است. 

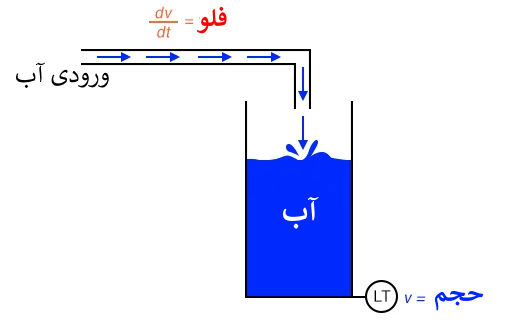
یک لِول ترانسمیتر (نشاندهنده سطح) که بر روی مخزن آب نصب شده باشد، سیگنالی متناسب با سطح آب در مخزن را ارائه می دهد، که اگر مخزن دارای سطح مقطع ثابتی باشد، می توانیم آن را با حجم آب ذخیره شده یکی فرض کنیم. اگر از این سیگنال بر حسب زمان مشتق بگیریم (dv/dt)، یک سیگنال متناسب با دبی جریان آب خروجی مخزن بدست می آوریم. مشتق گیری که بدین گونه که متصل شده باشد، سیگنال خروجی متناسب با دبی ایجاد می کند و احتمالاً می تواند جایگزین فلوترانسمیتر نصب شده در داخل لوله ورودی باشد. 

برگردیم به آزمایش خودرو. فرض کنید خودرو فرضی ما بر روی یکی از چرخهایش یک تاکوژنراتور داشته باشد که سیگنال ولتاژی متناسب با سرعت تولید کند. می توانیم از این سیگنال برای بدست آوردن شتاب با یک مدار مشتق گیر استفاده کنیم، مانند این: 

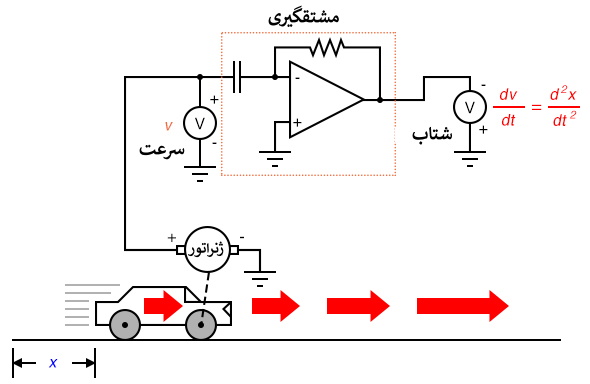
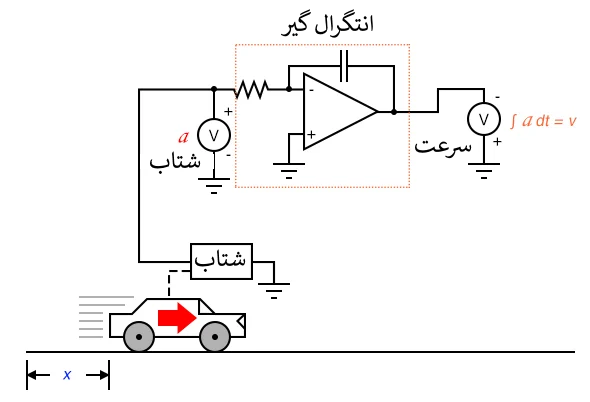
تاکوژنراتور بر اساس ماهیت خود از موقعیت خودرو نسبت به زمان مشتق می گیرد و ولتاژی متناسب با سرعت زاویه ای چرخ ایجاد می کند. تاکوژنراتور سیگنال خامی را به دست می دهد که قبلا نمایانگر سرعت بود و تنها با یک مرحله مشتق گیری سیگنال شتاب را به دست می دهد. دستگاه اندازه گیری سرعت با تاکوژنراتور در آلات دقیق خودرو بسیار عملی تر است از یک پتانسیومتر غول پیکر که موقعیت فیزیکی آن را اندازه گیری می کند، اما با آنچه که در عمل به دست می آوریم توانایی اندازه گیری موقعیت را از دست می دهیم. مهم نیست که چند بار مشتق گیری کنیم، هرگز نمی توانیم موقعیت خودرو را از سیگنال سرعت استنباط کنیم. اگر فرآیند مشتق گیری ما را از موقعیت به سرعت و از آنجا به شتاب می رساند، به نوعی لازم است تا فرایند "معکوس" مشتق گیری را انجام دهیم تا از سرعت به موقعیت برسیم. چنین فرآیندی وجود دارد و به آن انتگرال گیری می گویند. ممکن است از مدار "انتگرال گیر" برای انتگرال گیری نسبت به زمان استفاده شود. 

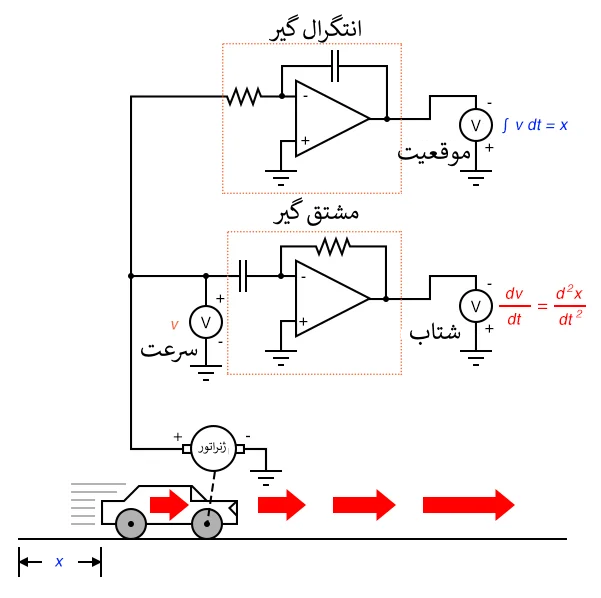
از آخرین فصل به یادآورید که مدار انتگرال گیر ولتاژی را به دست می دهد که نرخ تغییر آن نسبت به زمان متناسب با دامنه ولتاژ ورودی است. بنابراین، با اعمال یک ولتاژ ثابت به ورودی، ولتاژ خروجی با نرخی ثابت تغییر می کند. اگر خودرو با سرعتی ثابت حرکت کند (ولتاژ ثابتی از تاکوژنراتور به ورودی مدار انتگرال گیر اعمال می شود) ، پس مسافت طی شده به طور پیوسته نسبت به زمان افزایش می یابد، و انتگرال گیر ولتاژی با تغییرات ثابت متناسب با موقعیت به دست می دهد. اگر سرعت خودرو ثابت نباشد، خروجی انتگرال گیر دیگر نرخ جابجایی نسبت به زمان نخواهند بود، بلکه ولتاژ خروجی مسافت طی شده خودرو در هر لحظه را به دست می دهد. 

نماد انتگرال چیزی شبیه به یک حرف S باریک و بازشده است. معادله ای که از این نماد استفاده می کند (v.dt=x∫) به ما می گوید که ما از سرعت (v)  نسبت به زمان (dt) انتگرال گرفتیم تا موقعیت (x) را بدست آوریم. 

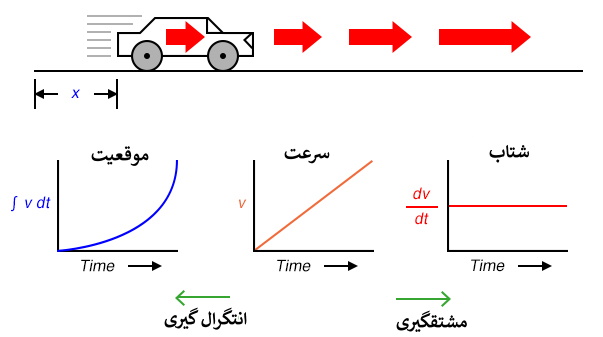
بنابراین، ما می توانیم سه کمیت جابجایی خودرو (موقعیت، سرعت و شتاب) را بر اساس سرعت (v) بیان کنیم به همان راحتی که می توانیم بر اساس موقعیت (x) چنین کنیم. 

اگر ما شتاب سنجی به خودرو وصل کرده بودیم که سیگنالی متناسب با افزایش یا کاهش شتاب ایجاد می کرد، (به صورت فرضی) می توانستیم سیگنال سرعت را با یک مرحله انتگرال گیری و سیگنال موقعیت را با دومین مرحله انتگرال گیری بدست آوریم. 

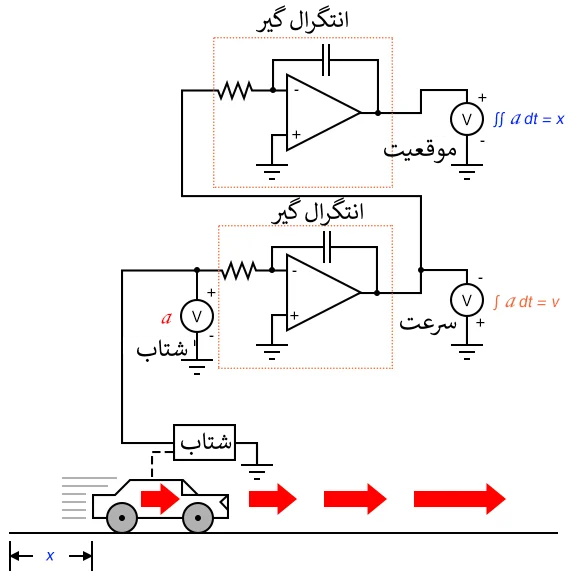
بنابراین، هر سه کمیت جابجایی خودرو (موقعیت، سرعت و شتاب) ممکن است بر اساس شتاب بیان شوند. 

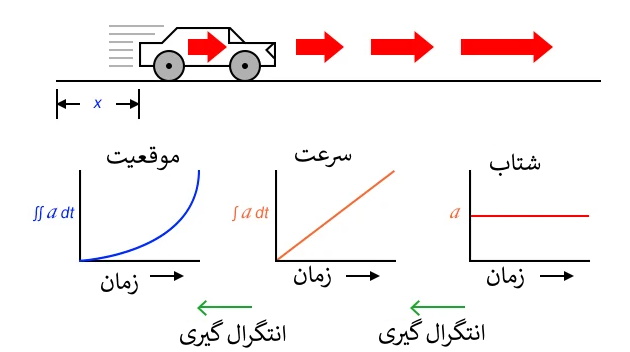
همانطور که احتمال داده اید، فرایند انتگرال گیری ممکن است در سایر سیستم های فیزیکی نیز نشان داده و یا در مورد آنها اعمال شود. برای مثال مخزن ذخیره آب و فلو را، که قبلاً نشان داده شد، در نظر بگیرید. اگر مشتق حجم مخزن نسبت به زمان نرخ فلو باشد  (q=dv/dt)، می توان گفت که حجم  انتگرال فلو نسبت به زمان است. 

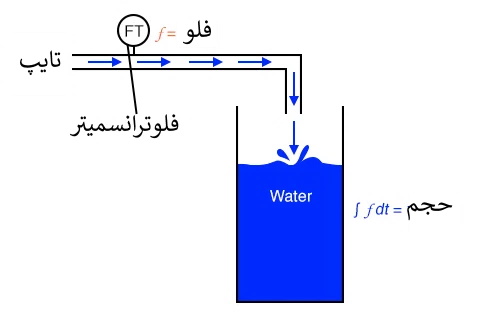
اگر بخواهیم از یک "فِلو ترانسمیتر" برای اندازه گیری جریان آب استفاده کنیم، با انتگرال گیری نسبت به زمان می توانیم حجم آب انباشته شده در مخزن را در طول زمان محاسبه کنیم. اگرچه از نظر تئوری می توان از ظرفیت یک انتگرال گیر ساخته شده از تقویت کننده های عملیاتی برای مشتق گرفتن یک سیگنال حجم از سیگنال فِلو استفاده کرد، اما انتگرال گیرهای مکانیکی و دیجیتالی برای انتگرال گیری در مدت زمان طولانی مناسب ترند و در شبکه های تصفیه و توزیع آب برای خود جای پایی بازکرده اند. 

همانطور که تکنیک های نمادینی برای مشتق گیری وجود دارند، تکنیک های نمادینی هم برای انتگرال گیری وجود دارند، اگرچه آنها پیچیده تر و متنوع تر هستند. استفاده از انتگرال گیر نمادین برای حل یک مسئله در دنیای واقعی، مانند شتاب خودرو، همچنان به در دسترس بودن معادله ای که سیگنال اندازه گیری شده را دقیقاً توصیف کند وابسته است. غالباً مشتق گرفتن از داده های اندازه گیری شده دشوار یا غیرممکن است. با این حال، انتگرال گیرهای الکترونیکی این عملکرد ریاضی را برای هر سیگنال ورودی به طور مداوم و در زمان واقعی انجام می دهند، بنابراین ابزاری قدرتمند برای دانشمندان و مهندسان فراهم می کنند. 

مدارات محاسبه کننده آنالوگ؛ قسمت اول

مترجم رضا کیانی موحد

منبع

https://www.allaboutcircuits.com/textbook/semiconductors/chpt-9/computational-circuits/

هنگامی که کسی کلمه "کامپیوتر" را ذکر می کند، یک دستگاه دیجیتال اولین چیزی است که معمولا به ذهن می رسد. مدارهای دیجیتال مقادیر عددی را در فرمت باینری نشان می دهند: الگوهای 1 و 0 توسط بسیاری از مدارهای ترانزیستوری که در حالت اشباع یا قطع هستند نشان داده می شوند. با این حال، مدارهای آنالوگ نیز می توانند برای نشان دادن مقادیر عددی و انجام محاسبات ریاضی، با استفاده از سیگنال های ولتاژ متغیر به جای حالت های روشن/خاموش (گسسته) به کار گرفته شوند.

در اینجا یک مثال ساده از نمایش دودویی (دیجیتال) در مقابل نمایش آنالوگ عدد "بیست و پنج" نشان داده شده است:

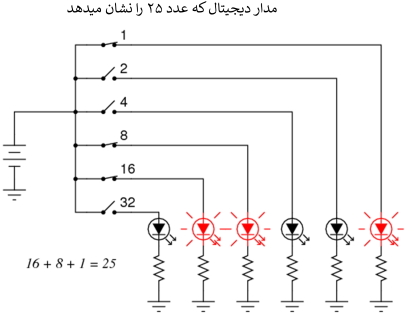
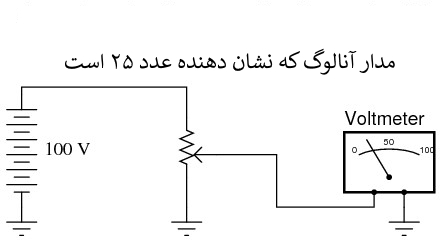
 مدارهای دیجیتال بسیار متفاوت از مدارهای آنالوگ هستند.

مدارهای محاسباتی دیجیتال می توانند فوق العاده پیچیده باشند و اغلب، محاسبات باید در مراحل متوالی انجام شوند تا پاسخ نهایی را بدست آورند، شبیه به یک انسان محاسبات ریاضی را مرحله به مرحله با مداد و کاغذ انجام می دهد. از سوی دیگر، در مقایسه با مدارهای دیجیتال، مدارهای محاسباتی آنالوگ بسیار ساده هستند و محاسبات خود را در حالت مداوم و در زمان واقعی انجام می دهند. یک مشکل برای استفاده از مدارهای آنالوگ برای نشان دادن اعداد وجود دارد: عدم دقت. مدار دیجیتالی که در بالا نشان داده شده است، دقیقا به عدد بیست و پنج اشاره دارد. مدار آنالوگ نشان داده شده در بالا ممکن است (یا ممکن نیست) به طور دقیق بر روی 25 ولت کالیبره شده باشد، اما این موضوع به "رانش" و خطا مربوط است.

در کاربردهایی که دقت خیلی مهم نیست، مدارهای محاسباتی آنالوگ بسیار عملی و مناسب هستند. در اینجا چند مدار ساخته شده از تقویت کننده های عملیاتی برای انجام محاسبات آنالوگ نشان داده شده است:

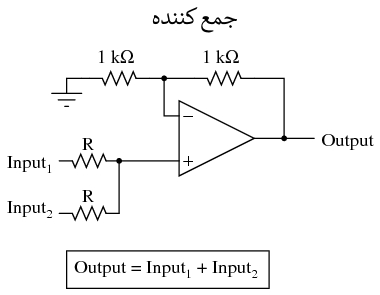
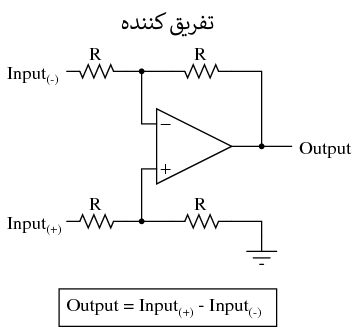
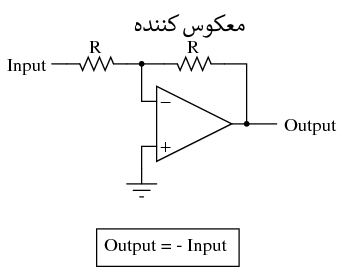
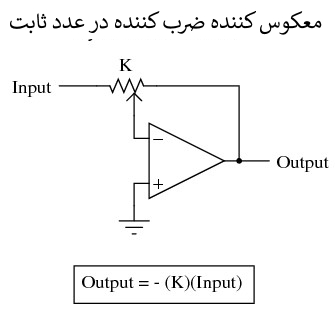
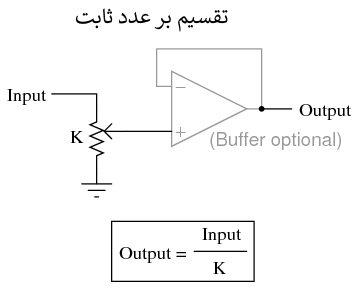
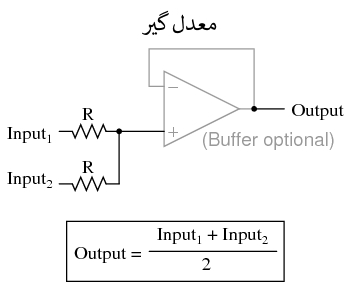
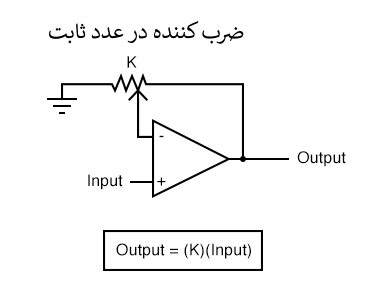
برای محاسبات پیچیده تر، هر یک از این مدارها می تواند به صورت ماجولار ب استفاده شوند تا مدار بزرگتری ایجاد شود. به عنوان مثال، فرض کنید که ما نیاز به کم کردن کسری از یک متغیر را از متغیر دیگری داریم. با ترکیب یک مدار تقسیم بر عددی ثابت با یک مدار تفریق کننده، می توانیم عملکرد مورد نیاز را بدست آوریم:

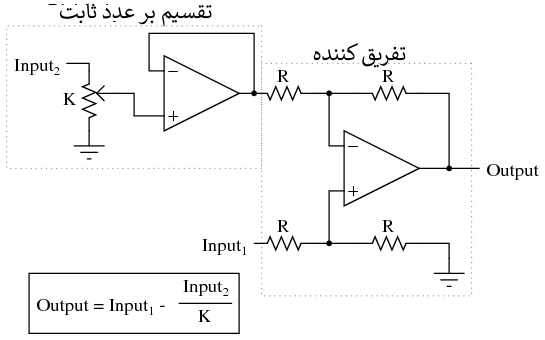
قبلا دستگاههایی که "کامپیوترهای آنالوگ" نامیده می شوند، در دانشگاه ها و مغازه های مهندسی رایج بودند. برای مدلسازی ریاضی، معمولا با هدف شبیه سازی برخی از فرآیندهای فیزیکی که معادلات اساسی آنها شناخته شده بود، در این کامپیوترهای آنالوگ ده ها مدار تقویت کننده عملیاتی می توانستند با اتصالات موقت به هم وصل شوند. کامپیوترهای دیجیتال کامپیوترهای آنالوگ را به کلی منسوخ کرده اند، اما مدارهای محاسباتی آنالوگ را نمی توان، از نظر ظرافت و صرفه جویی در اجزای ضروری، به خاطر مدارهای دیجیتال کنار گذاشت.

مدارهای محاسباتی آنالوگ، با استفاده از خازن در یک حلقه فیدبک یک تقویت کننده عملیاتی، در عملیات حسابی انتگرال گیری و مشتق گیری در طول زمان برتر هستند. با این حال، برای درک عملکرد و کاربردهای این مدارات، ابتدا باید معنای اساسی این مفاهیم محاسباتی را درک کنیم. خوشبختانه، استفاده از مدارهای تقویت کننده عملیاتی برای حل مشکلات محاسباتی جهان واقعی، به عنوان یک ابزار عالی برای تدریس حساب پایه به کار می رود. به گفته جان یاس اسمیت در کتاب آموزش عالی طراحی مدارات عملیاتی مدرن:

"یادداشت تشویقی برای خوانندگان راستین: محاسبات انتگرالی یکی از شاخه های ریاضی است که از تقویت کننده های عملیاتی بهره می برد و، در عمل، موانع فهم را از پیش پای برمی دارد."

احساسات آقای اسمیت در مورد ارزش آموزشی مدارهای آنالوگ به عنوان یک ابزار آموزشی در ریاضیات منحصر به فرد نیست. در نظر بگیرید نظریات مهندس جورج فاکس لنگ را در مقاله ای که برای شماره آگوست 2000 نشریه صدا و لرزش نوشته است:

"آنالوگ یک علامت تجاری کامپیوتر نبود! ایجاد یک موجود فیزیکی واقعی (یک مدار) تحت هدایت مجموعه ای از معادلات خاص و در تعامل با آنها، بصیرت منحصر به فردی را به آن معادلات ریاضی می دهد. برای بسط یک شهود درباره تأثیر متقابل بین فیزیک و ریاضیات، هیچ راهی بهتری از تجربه چنین تعاملی وجود ندارد. کامپیوتر آنالوگ ابزار قدرتمند بین رشته ای بود که بسیاری از اساتید در حوزه های گوناگون در ماتم فقدان آن هستند."

مشتق گیری اولین عملیاتی است که معمولا در شروع حساب توسط دانش آموزان یاد گرفته می شود. به عبارت ساده، مشتق گیری تعیین نرخ تغییر لحظه ای یک متغیر است نسبت به یک متغیر دیگر. در مدارهای مشتق گیر آنالوگ، متغیر مستقل زمان است و بنابراین نرخ تغییراتی که با آن برخورد می کنیم نرخ تغییر سیگنال الکترونیکی (ولتاژ یا جریان) است نسبت به زمان است.

فرض کنید ما قرار است تا موقعیت یک خودرو را اندازه بگیریم که از نقطه شروع و در مسیر مستقیم (بدون چرخش یا گردش) حرکت می کند. اجازه بدهید تا این اندازه را X نام دهیم. اگر خودرو با نرخی حرکت کند به طوری که فاصله آن از " نقطه شروع" به طور پیوسته در طول زمان افزایش بیابد، موقعیت آن به عنوان یک تابع خطی (خط مستقیم) رسم می شود:

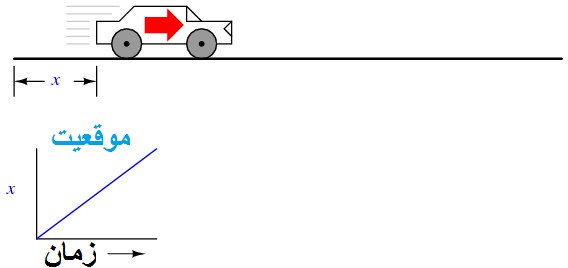
اگر مشتق موقعیت خودرو نسبت به زمان (یعنی تعیین نرخ جابجایی موقعیت خودرو نسبت به زمان) را محاسبه کنیم، به سرعت خودرو می رسیم. مشتق تابع با نماد کسری d/d  نشان داده می شود، بنابراین وقتی مشتق موقعیت (x) را نسبت به زمان (t) می گیریم، نتیجه (مشتق) را به شکل  dx/dtنمایش می دهیم.

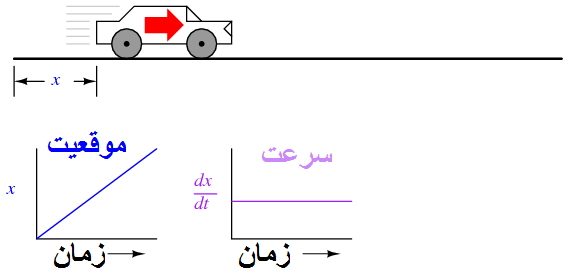
مشتق تابع خطیx  نسبت به زمان، مثلا مشتق موقعیت  (dx/dt)که معمولا سرعت نامیده می شود، یک خط صاف بدون تغییر است. مشتق یک تابع ریاضی هنگام رسم بر روی نمودار می تواند به صورت شیبدار نمایش داده شود، و در اینجا می توانیم ببینیم که نمودار موقعیت(x)  دارای یک شیب ثابت است، به این معنی که مشتق آن (dx/dt) باید نسبت به زمان ثابت باشد.

فرض کنیم که موقعیت خودرو نسبت به زمان به صورت نمایی افزایش بیابد: یعنی سفر خود را با حرکت آهسته شروع کرده، اما درهر دوره زمانی فاصله بیشتری را طی می کند. می بینیم که مشتق موقعیت (dx/dt)، یا همان سرعت(v) ، در طول زمان ثابت نبوده و افزایش می یابد.

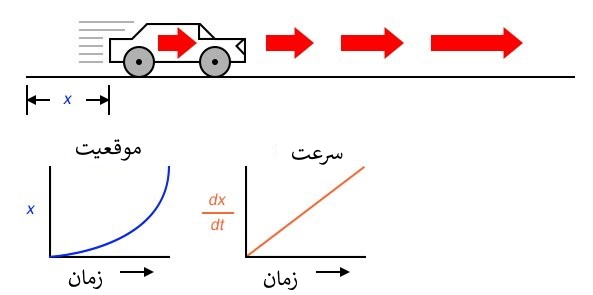
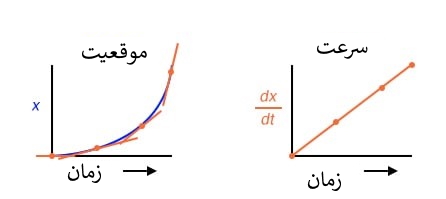
ارتفاع نقاط در نمودار سرعت متناظر است با نرخ تغییر (شیب) نقاط متناظر همان نقاط در نمودار موقعیت است.

این مسائل با مدارهای الکترونیکی آنالوگ چه ربطی دارند؟ خوب، اگر ما یک سیگنال ولتاژ آنالوگ داشته باشیم که نشان دهنده موقعیت خودرو باشد (تصور کنید یک پتانسیومتر بزرگ داریم که سر وسط آن به خودرو متصل است و ولتاژی متناسب با موقعیت خودرو  می سازد)، می توانیم یک مدار مشتق گیر به این سیگنال وصل کنیم و مداری داشته باشیم که به طور ثابت سرعت خودرو را محاسبه می کند و آن را از طریق یک ولت‌متر متصل به خروجی مدار مشتق گیر نشان می دهد.

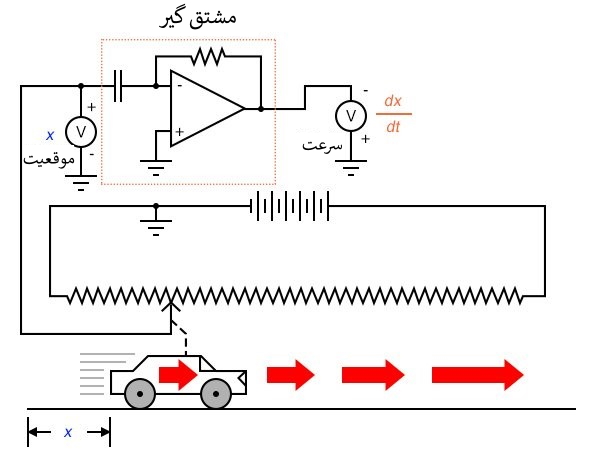
به یاد داشته باشید که خروجی یک مشتق گیر ولتاژی متناسب با نرخ تغیرات ولتاژ ورودی نسبت به زمان(d/dt)  است. بنابراین، اگر ولتاژ ورودی در طول زمان با نرخ ثابتی تغییر کند، ولتاژ خروجی یک دامنه ثابت خواهد داشت. اگر خودرو به گونه ای حرکت کند که فاصله طی شده نسبت به زمان نرخ ثابتی داشته باشد، به این معنی است که خودرو با سرعت ثابت حرکت می کند و مشتق گیر یک ولتاژ ثابت متناسب با سرعت را به خروجی می دهد. اگر فاصله طی شده توسط خودرو در طول زمان با نرخ غیر ثابتی تغییر کند، خروجی مدار مشتق گیر نیز غیر ثابت، اما متناظر با نرخ تغییرات ورودی نسبت به زمان، خواهد بود.

طراحی آسانسور با رویکرد دیجیتال، قسمت ششم

قسمت اول

قسمت دوم

قسمت سوم

قسمت چهارم

قسمت پنجم

دو تا پیچ اصلی در طراحی مدار فرمان برای آسانسور ساختمون چار طبقه رو رد کردیم و مونده دو تا پیچ دیگه: طراحی مدار فرمان وقتی که اتاقک آسانسور توی طبقه ی دومه و وقتی که توی طبقه ی سومه.

باز دوباره جدول صحت خروجی ها رو میکشیم ولی باید یادمون باشه که بر خلاف دو تا مدار قبلی (قسمت پنجم) اینبار کنتاکتورهای upp و downn روشن هستند و باید در جدول بیان. فقط چون هر کدوم روشن باشه اون یکی خاموشه میتونیم جدول رو ساده ش کنیم و یه بار برای upp=1 بنویسیم و یه بارم برای downn=1. دست آخر هم باید یادمه باشه که کنتاکتهای باز  s2 و upp (یا down) رو باید در مدار طراحی شده سری بکنیم:

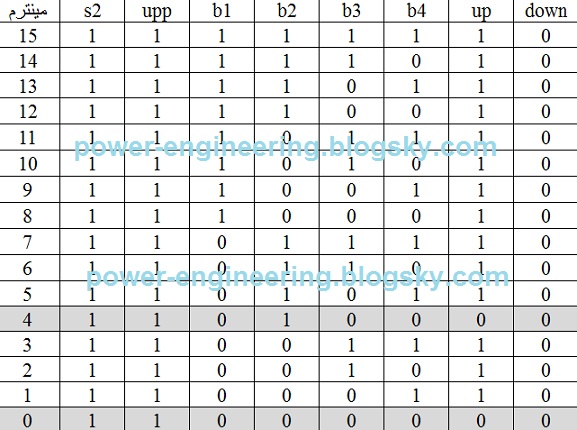
همون طور که دیده میشه وقتی که کلیدهای طبقات مختلف رو می زنیم فقط در مینترهای 4ام و 0ام هست که آسانسور حرکتی نمی کنه. در بقیه ی موارد اتاقک آسانسور باید بره بالا چون upp=1( اینکه چرا باید بره بالا رو قبلا مفصل توضیح ش دادیم). پیاده کردن جدول به صورت زیر در میادش:

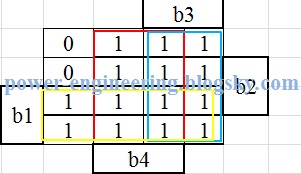
که یعنی:

up=b1+b3+b4

و همون طور که گفتیم باید دو تا ترم دیگه هم ضرب در حاصل جمع بکنیم یعنی:

up=s2.upp.(b1+b3+b4)

برای وقتی که downn=1 هست هم جدول زیر رو داریم:

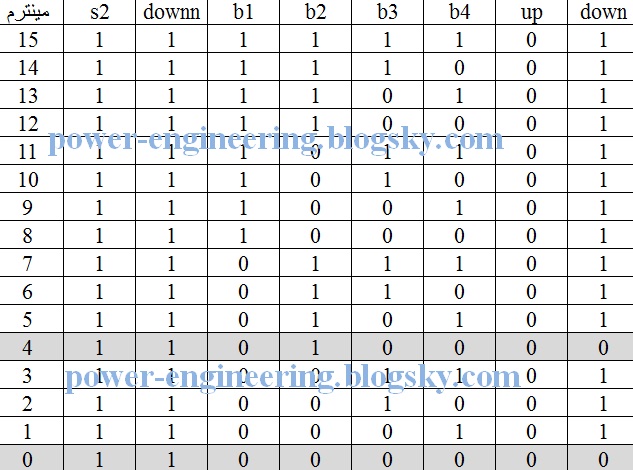
که بازم مینترمهای 4ام و 0ام برابر با صفر هستند و در نتیجه جدول حاصل مساوی جدول بالا می شه. فقط در جدول بالا باید upp رو ضرب می کردیم و حالا باید یادمون باشه که downn رو ضرب کنیم، یعنی :

down=s2.downn.(b1+b3+b4)

و مدار طراحی شده برای وقتی که اتاقک آسانسور در طبقه ی دومه به شکل زیر در میادش:

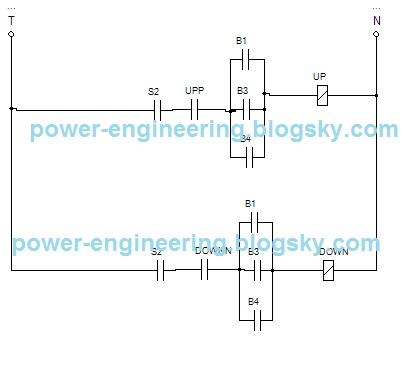
حالا بریم سراغ وضعیتی که اتاقک آسانسور در طبقه ی سوم قرار داشته باشه. در این حالت بازهم باید در نظر داشته باشیم که upp یا downn (یکی شون البته) می تونه که روشن باشه و باید در جدول بیادش. پس بازم دو تا جدول درست می کنیم. در حالت اول فرض میکنیم که upp=1 پس داریم:

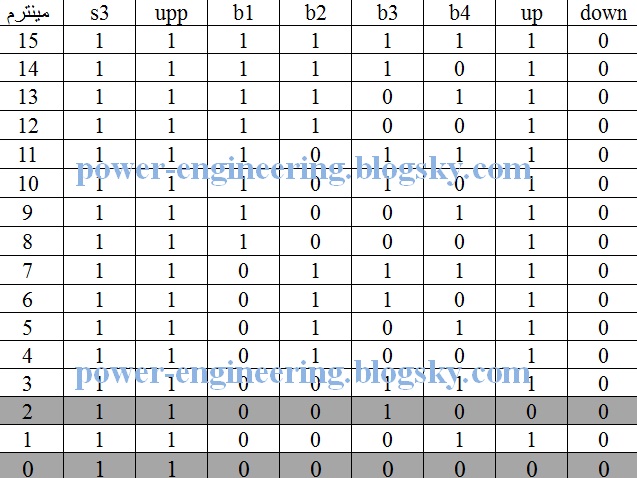
این بار مینترمهای دوم و 0ام برابر با صفر هستند و جدول حاصل برای خروجی up میشه:

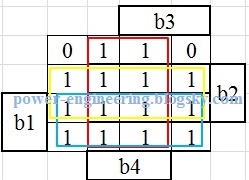
که یعنی :

up=b1+b2+b4

و چون باید تاثیر  s3 و upp رو هم در نظر داشته باشیم داریم:

up=s3.upp.(b1+b2+b4)

جدول وضعیت خروجی های وقتی که downn=1 باشه میشه:

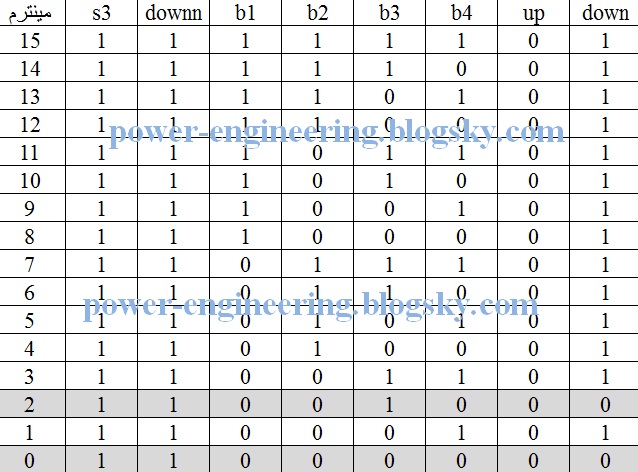
 که خلاصه ش میشه دقیقا برابر با جدول قبلی با این تفاوت که اینجا downn=1 هست. پس داریم:

down=s3.downn.(b1+b2+b4)

و نقشه ی مدار فرمان برای وضعیتی که اتاقک آسانسور در طبقه ی سوم هستش میشه:

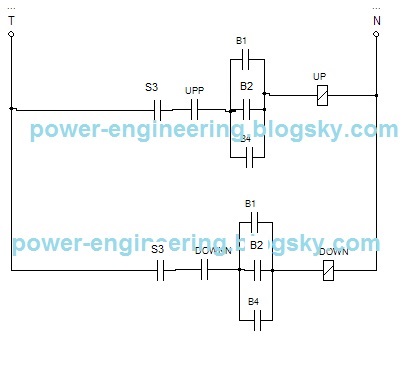
خوب دیگه. کار تمومه. حالا باید بیاییم و قضیه رو جمع ش کنیم. یعنی دو تا نقشه ی این قسمت با نقشه ی قسمت قبل که این هست

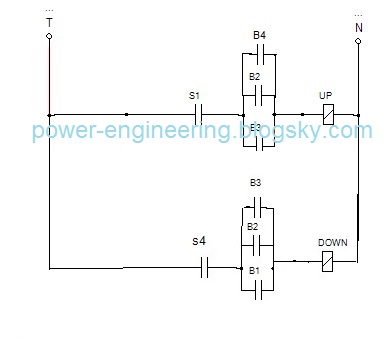
ترکیبشون کنیم توی یه نقشه که دقیقا میشه همون نقشه ی انتهای قسمت چهارم یعنی این:

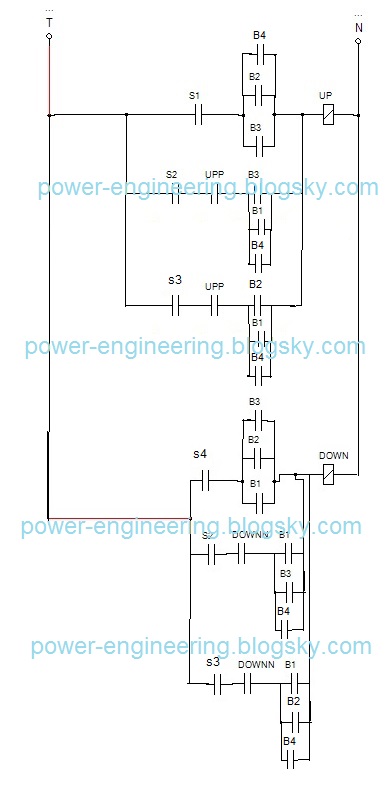
یعنی اگه منطق قضیه رو خوب فهمیده باشید هیچ فرقی نمیکنه که مدارتون رو به صورت معمولی طراحی کنید یا با استفاده از منطق دیجیتال. همین مدار رو البته موقع پیاده سازی می تونید با گیتهای دیجیتالی هم پیاده کنید یعنی کنتاکتهای سری رو به جاشون گیت AND بذارید و کنتاکتهای موازی رو گیت OR و خروجی رو هم بدید به یه رله که اون رله بیادش و کنتاکتورهاتون رو راه اندازی کنه. البته یه سری مسائل و مشکلات هم در زمینه ی نویز و این حرفها خواهید داشت که بهتره کلا قضیه رو بیخیال شید و از همین کنتاکتور و اینها استفاده کنیم.

حالا که منطق قضیه رو خوب فهمیدید دیگه طراحی مدار فرمان برای ساختمان های بلندتر از چار طبقه خیلی سخت نیست. فقط یه کم فشار باس بیارید به مغزتون.

قسمت ششم بحث طراحی مدار فرمان آسانسور در حالی تموم شده که الان فک میکنید دیگه اوستا شدید ولی اشتباه می کنید. ما تا حالا فقط یادتون دادیم که چطور آسانسور رو راهش بندازید. هنوز نگفتیم که وقتی راه افتاد چه طوری باید متوقف ش بکنید. پس ، با ما باشید.

قسمت هفتم

قسمت هشتم

قسمت نهم

قسمت دهم