
برق-قدرت
اینجا فقط از برق و الکترونیک و کامپیوتر حرف می زنیم
برق-قدرت
اینجا فقط از برق و الکترونیک و کامپیوتر حرف می زنیممدارات محاسبه کننده آنالوگ؛ قسمت اول
مترجم رضا کیانی موحد
منبع
https://www.allaboutcircuits.com/textbook/semiconductors/chpt-9/computational-circuits/
هنگامی که کسی کلمه "کامپیوتر" را ذکر می کند، یک دستگاه دیجیتال اولین چیزی است که معمولا به ذهن می رسد. مدارهای دیجیتال مقادیر عددی را در فرمت باینری نشان می دهند: الگوهای 1 و 0 توسط بسیاری از مدارهای ترانزیستوری که در حالت اشباع یا قطع هستند نشان داده می شوند. با این حال، مدارهای آنالوگ نیز می توانند برای نشان دادن مقادیر عددی و انجام محاسبات ریاضی، با استفاده از سیگنال های ولتاژ متغیر به جای حالت های روشن/خاموش (گسسته) به کار گرفته شوند.
در اینجا یک مثال ساده از نمایش دودویی (دیجیتال) در مقابل نمایش آنالوگ عدد "بیست و پنج" نشان داده شده است:
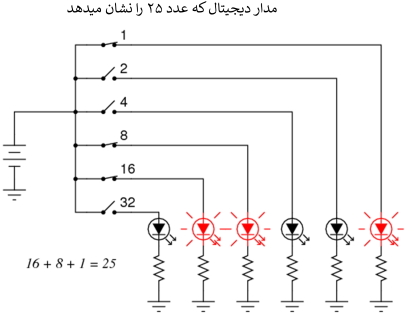
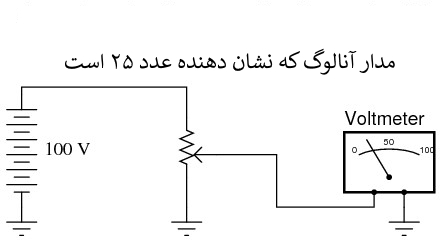
مدارهای دیجیتال بسیار متفاوت از مدارهای آنالوگ هستند.
مدارهای محاسباتی دیجیتال می توانند فوق العاده پیچیده باشند و اغلب، محاسبات باید در مراحل متوالی انجام شوند تا پاسخ نهایی را بدست آورند، شبیه به یک انسان محاسبات ریاضی را مرحله به مرحله با مداد و کاغذ انجام می دهد. از سوی دیگر، در مقایسه با مدارهای دیجیتال، مدارهای محاسباتی آنالوگ بسیار ساده هستند و محاسبات خود را در حالت مداوم و در زمان واقعی انجام می دهند. یک مشکل برای استفاده از مدارهای آنالوگ برای نشان دادن اعداد وجود دارد: عدم دقت. مدار دیجیتالی که در بالا نشان داده شده است، دقیقا به عدد بیست و پنج اشاره دارد. مدار آنالوگ نشان داده شده در بالا ممکن است (یا ممکن نیست) به طور دقیق بر روی 25 ولت کالیبره شده باشد، اما این موضوع به "رانش" و خطا مربوط است.
در کاربردهایی که دقت خیلی مهم نیست، مدارهای محاسباتی آنالوگ بسیار عملی و مناسب هستند. در اینجا چند مدار ساخته شده از تقویت کننده های عملیاتی برای انجام محاسبات آنالوگ نشان داده شده است:
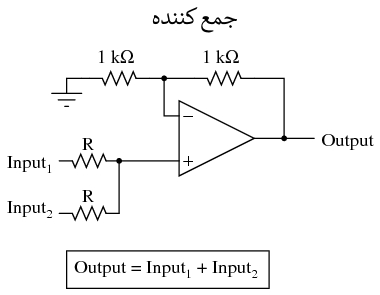
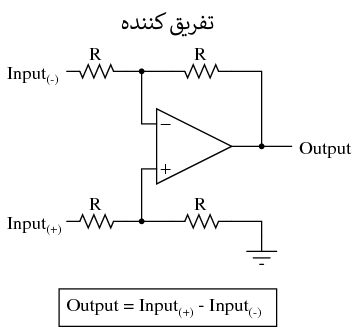
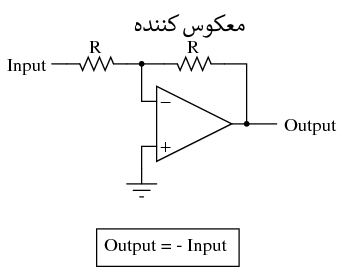
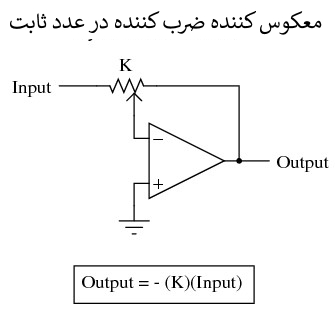
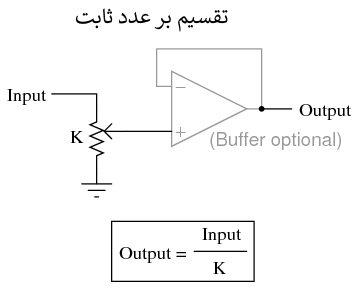
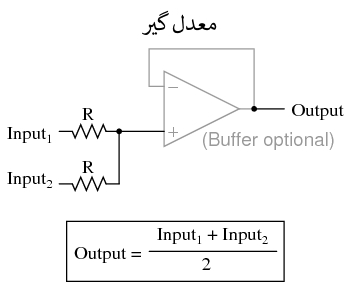
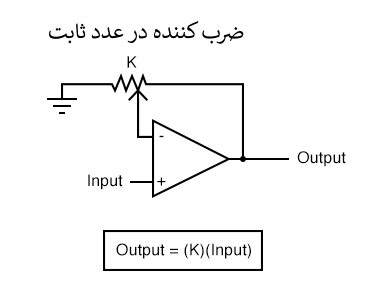
برای محاسبات پیچیده تر، هر یک از این مدارها می تواند به صورت ماجولار ب استفاده شوند تا مدار بزرگتری ایجاد شود. به عنوان مثال، فرض کنید که ما نیاز به کم کردن کسری از یک متغیر را از متغیر دیگری داریم. با ترکیب یک مدار تقسیم بر عددی ثابت با یک مدار تفریق کننده، می توانیم عملکرد مورد نیاز را بدست آوریم:
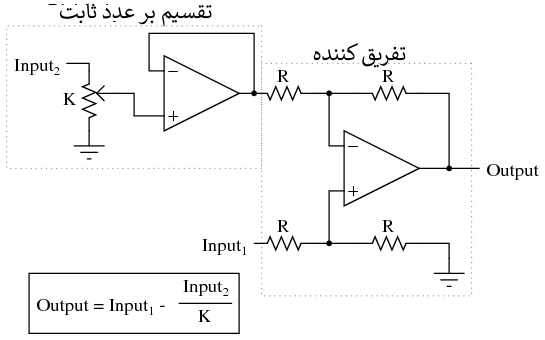
قبلا دستگاههایی که "کامپیوترهای آنالوگ" نامیده می شوند، در دانشگاه ها و مغازه های مهندسی رایج بودند. برای مدلسازی ریاضی، معمولا با هدف شبیه سازی برخی از فرآیندهای فیزیکی که معادلات اساسی آنها شناخته شده بود، در این کامپیوترهای آنالوگ ده ها مدار تقویت کننده عملیاتی می توانستند با اتصالات موقت به هم وصل شوند. کامپیوترهای دیجیتال کامپیوترهای آنالوگ را به کلی منسوخ کرده اند، اما مدارهای محاسباتی آنالوگ را نمی توان، از نظر ظرافت و صرفه جویی در اجزای ضروری، به خاطر مدارهای دیجیتال کنار گذاشت.
مدارهای محاسباتی آنالوگ، با استفاده از خازن در یک حلقه فیدبک یک تقویت کننده عملیاتی، در عملیات حسابی انتگرال گیری و مشتق گیری در طول زمان برتر هستند. با این حال، برای درک عملکرد و کاربردهای این مدارات، ابتدا باید معنای اساسی این مفاهیم محاسباتی را درک کنیم. خوشبختانه، استفاده از مدارهای تقویت کننده عملیاتی برای حل مشکلات محاسباتی جهان واقعی، به عنوان یک ابزار عالی برای تدریس حساب پایه به کار می رود. به گفته جان یاس اسمیت در کتاب آموزش عالی طراحی مدارات عملیاتی مدرن:
"یادداشت تشویقی برای خوانندگان راستین: محاسبات انتگرالی یکی از شاخه های ریاضی است که از تقویت کننده های عملیاتی بهره می برد و، در عمل، موانع فهم را از پیش پای برمی دارد."
احساسات آقای اسمیت در مورد ارزش آموزشی مدارهای آنالوگ به عنوان یک ابزار آموزشی در ریاضیات منحصر به فرد نیست. در نظر بگیرید نظریات مهندس جورج فاکس لنگ را در مقاله ای که برای شماره آگوست 2000 نشریه صدا و لرزش نوشته است:
"آنالوگ یک علامت تجاری کامپیوتر نبود! ایجاد یک موجود فیزیکی واقعی (یک مدار) تحت هدایت مجموعه ای از معادلات خاص و در تعامل با آنها، بصیرت منحصر به فردی را به آن معادلات ریاضی می دهد. برای بسط یک شهود درباره تأثیر متقابل بین فیزیک و ریاضیات، هیچ راهی بهتری از تجربه چنین تعاملی وجود ندارد. کامپیوتر آنالوگ ابزار قدرتمند بین رشته ای بود که بسیاری از اساتید در حوزه های گوناگون در ماتم فقدان آن هستند."
مشتق گیری اولین عملیاتی است که معمولا در شروع حساب توسط دانش آموزان یاد گرفته می شود. به عبارت ساده، مشتق گیری تعیین نرخ تغییر لحظه ای یک متغیر است نسبت به یک متغیر دیگر. در مدارهای مشتق گیر آنالوگ، متغیر مستقل زمان است و بنابراین نرخ تغییراتی که با آن برخورد می کنیم نرخ تغییر سیگنال الکترونیکی (ولتاژ یا جریان) است نسبت به زمان است.
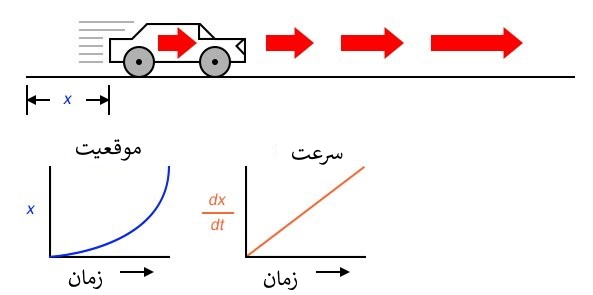
فرض کنید ما قرار است تا موقعیت یک خودرو را اندازه بگیریم که از نقطه شروع و در مسیر مستقیم (بدون چرخش یا گردش) حرکت می کند. اجازه بدهید تا این اندازه را X نام دهیم. اگر خودرو با نرخی حرکت کند به طوری که فاصله آن از " نقطه شروع" به طور پیوسته در طول زمان افزایش بیابد، موقعیت آن به عنوان یک تابع خطی (خط مستقیم) رسم می شود:
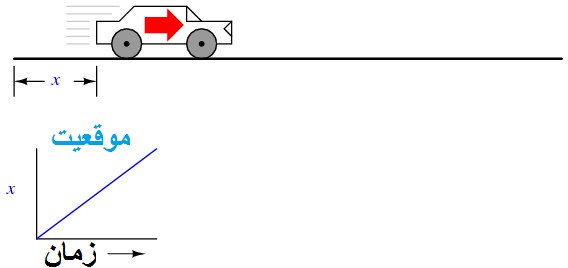
اگر مشتق موقعیت خودرو نسبت به زمان (یعنی تعیین نرخ جابجایی موقعیت خودرو نسبت به زمان) را محاسبه کنیم، به سرعت خودرو می رسیم. مشتق تابع با نماد کسری d/d نشان داده می شود، بنابراین وقتی مشتق موقعیت (x) را نسبت به زمان (t) می گیریم، نتیجه (مشتق) را به شکل dx/dtنمایش می دهیم.
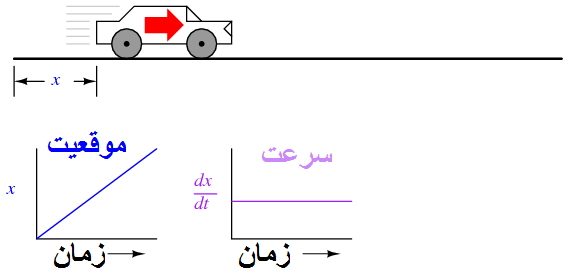
مشتق تابع خطیx نسبت به زمان، مثلا مشتق موقعیت (dx/dt)که معمولا سرعت نامیده می شود، یک خط صاف بدون تغییر است. مشتق یک تابع ریاضی هنگام رسم بر روی نمودار می تواند به صورت شیبدار نمایش داده شود، و در اینجا می توانیم ببینیم که نمودار موقعیت(x) دارای یک شیب ثابت است، به این معنی که مشتق آن (dx/dt) باید نسبت به زمان ثابت باشد.
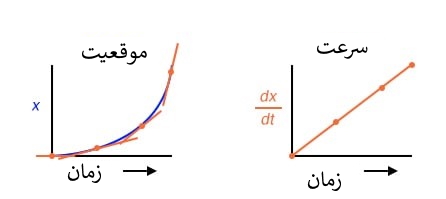
فرض کنیم که موقعیت خودرو نسبت به زمان به صورت نمایی افزایش بیابد: یعنی سفر خود را با حرکت آهسته شروع کرده، اما درهر دوره زمانی فاصله بیشتری را طی می کند. می بینیم که مشتق موقعیت (dx/dt)، یا همان سرعت(v) ، در طول زمان ثابت نبوده و افزایش می یابد.
ارتفاع نقاط در نمودار سرعت متناظر است با نرخ تغییر (شیب) نقاط متناظر همان نقاط در نمودار موقعیت است.
این مسائل با مدارهای الکترونیکی آنالوگ چه ربطی دارند؟ خوب، اگر ما یک سیگنال ولتاژ آنالوگ داشته باشیم که نشان دهنده موقعیت خودرو باشد (تصور کنید یک پتانسیومتر بزرگ داریم که سر وسط آن به خودرو متصل است و ولتاژی متناسب با موقعیت خودرو می سازد)، می توانیم یک مدار مشتق گیر به این سیگنال وصل کنیم و مداری داشته باشیم که به طور ثابت سرعت خودرو را محاسبه می کند و آن را از طریق یک ولتمتر متصل به خروجی مدار مشتق گیر نشان می دهد.
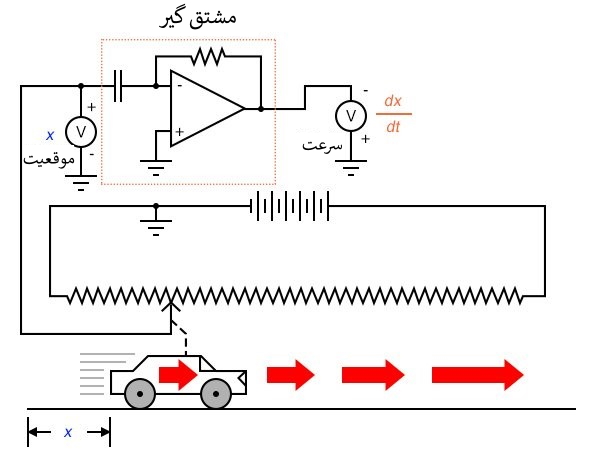
به یاد داشته باشید که خروجی یک مشتق گیر ولتاژی متناسب با نرخ تغیرات ولتاژ ورودی نسبت به زمان(d/dt) است. بنابراین، اگر ولتاژ ورودی در طول زمان با نرخ ثابتی تغییر کند، ولتاژ خروجی یک دامنه ثابت خواهد داشت. اگر خودرو به گونه ای حرکت کند که فاصله طی شده نسبت به زمان نرخ ثابتی داشته باشد، به این معنی است که خودرو با سرعت ثابت حرکت می کند و مشتق گیر یک ولتاژ ثابت متناسب با سرعت را به خروجی می دهد. اگر فاصله طی شده توسط خودرو در طول زمان با نرخ غیر ثابتی تغییر کند، خروجی مدار مشتق گیر نیز غیر ثابت، اما متناظر با نرخ تغییرات ورودی نسبت به زمان، خواهد بود.
نرم افزار شبیه ساز الکترونیک ورک بنچ

نرم افزار الکترونیک ورک بنچ (میز کار الکترونیک یا ewb) یک نرم افزار شبیه سازی قطعات الکترونیکی است که کار کردن با آن بسیار ساده است. این نرم افزار شاید به قدرت نرم افزارهای پیشرفته ای چون پورسئوس نباشد اما می توانید با آن بسیاری از مدارات ساده ی دیجیتال و آنالوگ را شبیه سازی کنید و نتیجه را بررسی کنید. این نرم افزار را می توانید از اینجا دانلود کنید. این فایل هم توضیحاتی درباره ی استفاده از آن داده است.