مدارات محاسبه کننده آنالوگ؛ قسمت دوم

توجه داشته باشید که سرعت ثبت شده توسط ولتمتر (در خروجی مدار مشتق گیر) با قطبیت "معکوس" در خروجی تقویت کننده عملیاتی ظاهر می شود. این امر به این دلیل است که مدار مشتق گیر نشان داده شده است معکوس کننده هم هست: به ازای یک ولتاژ مثبت در ورودی، یک ولتاژ منفی به خروجی اعمال می شود. اگر بخواهیم که ولتمتر مقداری مثبت را برای سرعت نشان بدهد، باید همانطور که در تصویر نشان داده شده، به تقویت کننده عملیاتی متصل شود. اگرچه غیرممکن است که پتانسیومتر غول پیکری به متحرکی مانند یک خودرو وصل شود، این مفهوم باید روشن شده باشد که: با انجام مشتق گیری بر روی سیگنال، که نمایشگر موقعیت فعلی است، به یک سیگنال نمایشگر سرعت دست یافته ایم. 

دانش آموزان در شروع فراگیری حساب دیفرانسیل روشهای ریاضی را برای مشتق گیری یاد می گیرند. با این وجود، لازم است که معادله توصیف کننده تابع اصلی شناخته شود. به عنوان مثال، دانش آموزان یاد می گیرند که چگونه مشتق یک تابع مانند y = 3x را  را به سادگی با دستکاری کردن معادله تابع پیدا کنند. می توانیم که دقت این دستکاریها را با مقایسه نمودار دو توابع بررسی کنیم: 

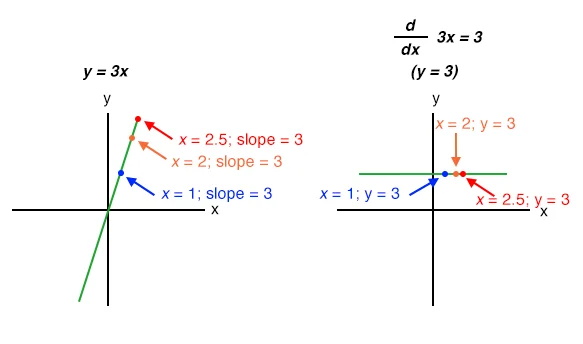
تابع غیرخطی مانند y=3x2 ممکن است که با روشهای ریاضی مشتق گیری شود. در این صورت مشتق برابر خواهد بود با 6x. 

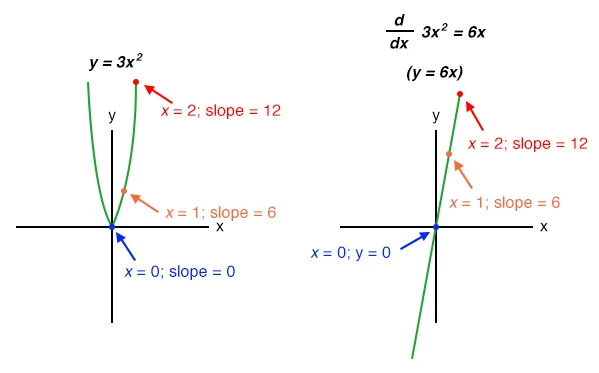
با این حال، در زندگی واقعی اغلب نمی توانیم رفتار یک رویداد فیزیکی را با یک معادله ی ساده مثل y = 3x توصیف کنیم، و بنابراین روشهای نمادین مشتق گیری دبیرستانی ممکن است برای اندازه گیری های فیزیکی غیرممکن باشد. اگر کسی بخواهد از موقعیت فرضی خودروی ما با روشهای ریاضی مشتق بگیرد(dx/dt=speed) ، ابتدا باید معادله ی موقعیت خودرو را با توجه به اندازه گیری موقعیت در یک آزمایش واقعی بدست آورد، امری که تقریبا غیرممکن است مگر اینکه خودرو تحت شرایط دقیق کنترل شده حرکت کند و منجر به ساخت یک نمودار ساده از موقعیت شود. با این حال، یک مدار مشتق گیر آنالوگ، با بهره گیری از رابطه ی خازن نسبت به ولتاژ، جریان و زمان i=C (dv/dt)، به طور طبیعی از هر سیگنال واقعی ولتاژ نسبت به زمان مشتق می گیرد، و می تواند سیگنالی متناسب با سرعت لحظه ای (dx/dt) را به دست دهد. با ترسیم سیگنال موقعیت خودرو نسبت به سیگنال خروجی مشتق گیر در یک نمودار، هر دو نمودار به طور طبیعی خود را برای تجزیه و تحلیل به نمایش می گذارند. 

می توانیم با اعمال سیگنال سرعت به یک مشتق گیر دیگر، مشتق گیری را یک گام دیگر به جلو ببریم. به عبارت دیگر، از آن برای محاسبه نرخ تغییر سرعت، که خودش نرخ تغییر موقعیت است، استفاده کنیم. برای عملی کردن این فکر چه اقدامی می توانیم انجام دهیم؟ به این امر از دید واحدهایی که برای اندازه گیری موقعیت و سرعت استفاده کردیم نگاه کنید. اگر برای تعیین موقعیت خودرو از نقطه شروع خود از مایل استفاده کنیم، احتمالا سرعت آن را با واحد مایل بر ساعت (dx/dt) بیان می کنیم. اگر از سرعت (با واحد مایل بر ساعت) نسبت به زمان مشتق بگیریم، به واحد مایل بر ساعت بر ساعت می رسیم. در فیزیک مقدماتی به دانش آموزان درباره سقوط آزاد می آموزند که اندازه گیری موقعیت با متر، سرعت با متر بر ثانیه و تغییر سرعت در طول زمان با متر بر ثانیه بر هر ثانیه انجام می شود. این آخری شتاب نامیده می شود: نرخ تغییر سرعت در واحد زمان. 

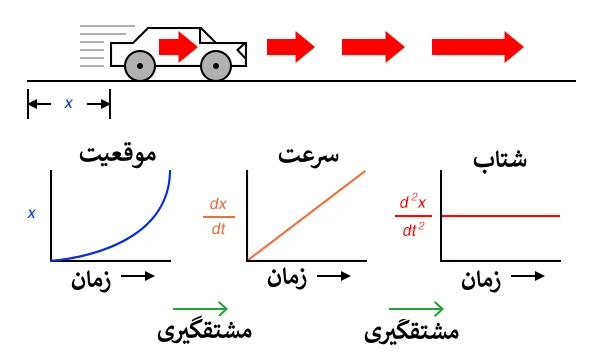
فرمول d2x/dt2 مشتق دوم موقعیت (x) نسبت به زمان (t) نامیده می شود. اگر مشتق گیر دوم را به خروجی اولی وصل کنیم، آخرین ولتمتر شتاب را ثبت می کند. 

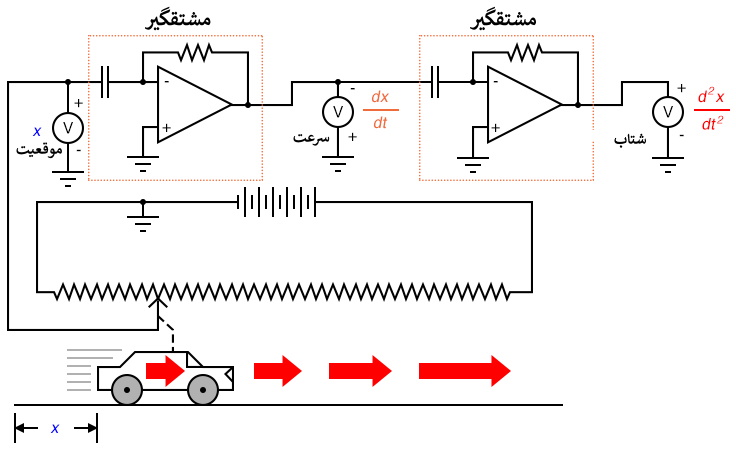
با به دست آوردن سرعت از موقعیت و شتاب از سرعت، اصول مشتق گیری را به وضوح می توانیم ببینیم. این ها شاید که تنها اندازه گیری های فیزیکی مرتبط با هم به این روش نباشند، اما شاید که شایع ترین آنها باشند. مثال دیگری از حساب دیفرانسیل در عمل رابطه بین جریان(q)  و حجم مایع (v) انباشته شده در یک مخزن نسبت به زمان است. 

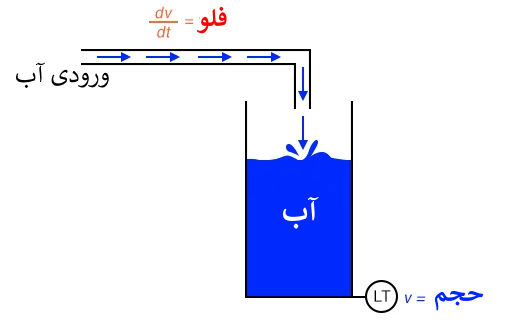
یک لِول ترانسمیتر (نشاندهنده سطح) که بر روی مخزن آب نصب شده باشد، سیگنالی متناسب با سطح آب در مخزن را ارائه می دهد، که اگر مخزن دارای سطح مقطع ثابتی باشد، می توانیم آن را با حجم آب ذخیره شده یکی فرض کنیم. اگر از این سیگنال بر حسب زمان مشتق بگیریم (dv/dt)، یک سیگنال متناسب با دبی جریان آب خروجی مخزن بدست می آوریم. مشتق گیری که بدین گونه که متصل شده باشد، سیگنال خروجی متناسب با دبی ایجاد می کند و احتمالاً می تواند جایگزین فلوترانسمیتر نصب شده در داخل لوله ورودی باشد. 

برگردیم به آزمایش خودرو. فرض کنید خودرو فرضی ما بر روی یکی از چرخهایش یک تاکوژنراتور داشته باشد که سیگنال ولتاژی متناسب با سرعت تولید کند. می توانیم از این سیگنال برای بدست آوردن شتاب با یک مدار مشتق گیر استفاده کنیم، مانند این: 

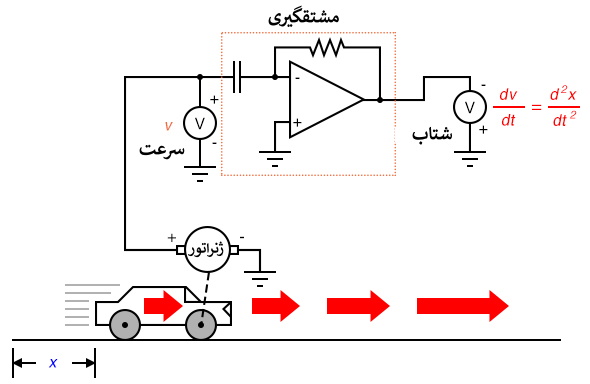
تاکوژنراتور بر اساس ماهیت خود از موقعیت خودرو نسبت به زمان مشتق می گیرد و ولتاژی متناسب با سرعت زاویه ای چرخ ایجاد می کند. تاکوژنراتور سیگنال خامی را به دست می دهد که قبلا نمایانگر سرعت بود و تنها با یک مرحله مشتق گیری سیگنال شتاب را به دست می دهد. دستگاه اندازه گیری سرعت با تاکوژنراتور در آلات دقیق خودرو بسیار عملی تر است از یک پتانسیومتر غول پیکر که موقعیت فیزیکی آن را اندازه گیری می کند، اما با آنچه که در عمل به دست می آوریم توانایی اندازه گیری موقعیت را از دست می دهیم. مهم نیست که چند بار مشتق گیری کنیم، هرگز نمی توانیم موقعیت خودرو را از سیگنال سرعت استنباط کنیم. اگر فرآیند مشتق گیری ما را از موقعیت به سرعت و از آنجا به شتاب می رساند، به نوعی لازم است تا فرایند "معکوس" مشتق گیری را انجام دهیم تا از سرعت به موقعیت برسیم. چنین فرآیندی وجود دارد و به آن انتگرال گیری می گویند. ممکن است از مدار "انتگرال گیر" برای انتگرال گیری نسبت به زمان استفاده شود. 

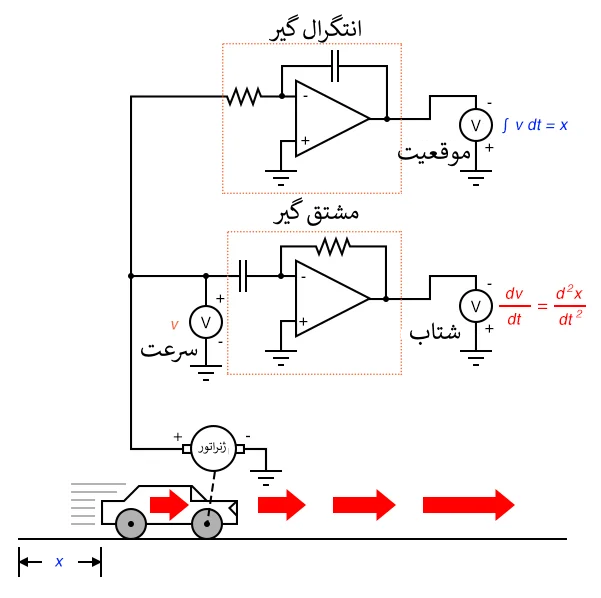
از آخرین فصل به یادآورید که مدار انتگرال گیر ولتاژی را به دست می دهد که نرخ تغییر آن نسبت به زمان متناسب با دامنه ولتاژ ورودی است. بنابراین، با اعمال یک ولتاژ ثابت به ورودی، ولتاژ خروجی با نرخی ثابت تغییر می کند. اگر خودرو با سرعتی ثابت حرکت کند (ولتاژ ثابتی از تاکوژنراتور به ورودی مدار انتگرال گیر اعمال می شود) ، پس مسافت طی شده به طور پیوسته نسبت به زمان افزایش می یابد، و انتگرال گیر ولتاژی با تغییرات ثابت متناسب با موقعیت به دست می دهد. اگر سرعت خودرو ثابت نباشد، خروجی انتگرال گیر دیگر نرخ جابجایی نسبت به زمان نخواهند بود، بلکه ولتاژ خروجی مسافت طی شده خودرو در هر لحظه را به دست می دهد. 

نماد انتگرال چیزی شبیه به یک حرف S باریک و بازشده است. معادله ای که از این نماد استفاده می کند (v.dt=x∫) به ما می گوید که ما از سرعت (v)  نسبت به زمان (dt) انتگرال گرفتیم تا موقعیت (x) را بدست آوریم. 

بنابراین، ما می توانیم سه کمیت جابجایی خودرو (موقعیت، سرعت و شتاب) را بر اساس سرعت (v) بیان کنیم به همان راحتی که می توانیم بر اساس موقعیت (x) چنین کنیم. 

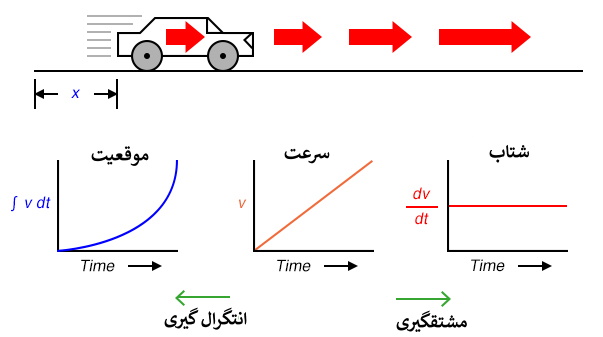
اگر ما شتاب سنجی به خودرو وصل کرده بودیم که سیگنالی متناسب با افزایش یا کاهش شتاب ایجاد می کرد، (به صورت فرضی) می توانستیم سیگنال سرعت را با یک مرحله انتگرال گیری و سیگنال موقعیت را با دومین مرحله انتگرال گیری بدست آوریم. 

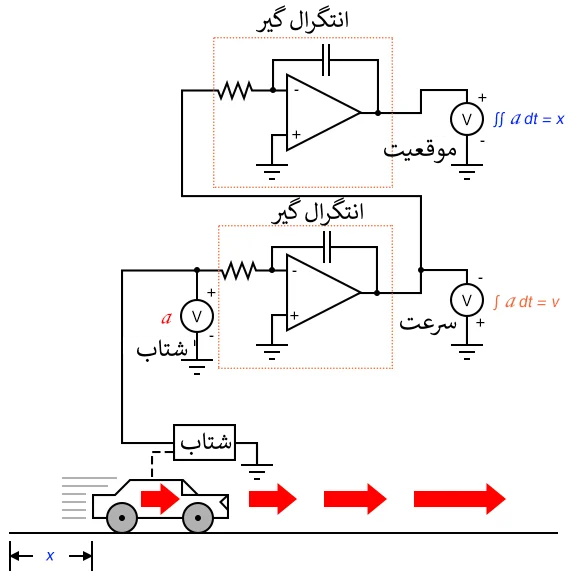
بنابراین، هر سه کمیت جابجایی خودرو (موقعیت، سرعت و شتاب) ممکن است بر اساس شتاب بیان شوند. 

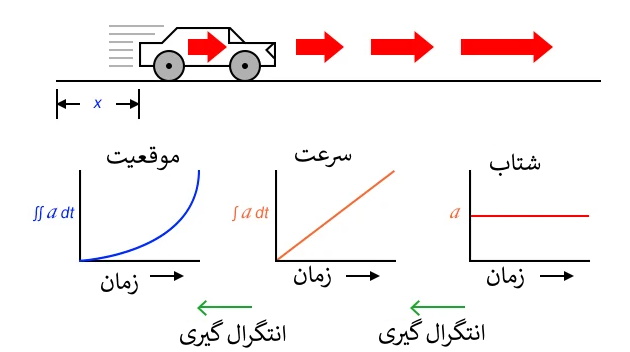
همانطور که احتمال داده اید، فرایند انتگرال گیری ممکن است در سایر سیستم های فیزیکی نیز نشان داده و یا در مورد آنها اعمال شود. برای مثال مخزن ذخیره آب و فلو را، که قبلاً نشان داده شد، در نظر بگیرید. اگر مشتق حجم مخزن نسبت به زمان نرخ فلو باشد  (q=dv/dt)، می توان گفت که حجم  انتگرال فلو نسبت به زمان است. 

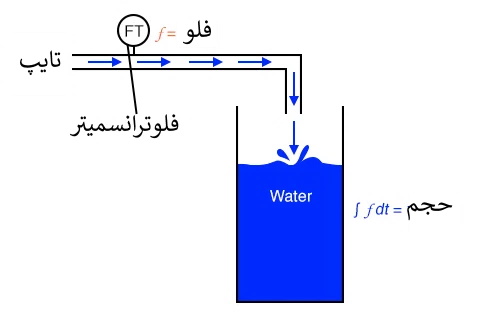
اگر بخواهیم از یک "فِلو ترانسمیتر" برای اندازه گیری جریان آب استفاده کنیم، با انتگرال گیری نسبت به زمان می توانیم حجم آب انباشته شده در مخزن را در طول زمان محاسبه کنیم. اگرچه از نظر تئوری می توان از ظرفیت یک انتگرال گیر ساخته شده از تقویت کننده های عملیاتی برای مشتق گرفتن یک سیگنال حجم از سیگنال فِلو استفاده کرد، اما انتگرال گیرهای مکانیکی و دیجیتالی برای انتگرال گیری در مدت زمان طولانی مناسب ترند و در شبکه های تصفیه و توزیع آب برای خود جای پایی بازکرده اند. 

همانطور که تکنیک های نمادینی برای مشتق گیری وجود دارند، تکنیک های نمادینی هم برای انتگرال گیری وجود دارند، اگرچه آنها پیچیده تر و متنوع تر هستند. استفاده از انتگرال گیر نمادین برای حل یک مسئله در دنیای واقعی، مانند شتاب خودرو، همچنان به در دسترس بودن معادله ای که سیگنال اندازه گیری شده را دقیقاً توصیف کند وابسته است. غالباً مشتق گرفتن از داده های اندازه گیری شده دشوار یا غیرممکن است. با این حال، انتگرال گیرهای الکترونیکی این عملکرد ریاضی را برای هر سیگنال ورودی به طور مداوم و در زمان واقعی انجام می دهند، بنابراین ابزاری قدرتمند برای دانشمندان و مهندسان فراهم می کنند.