مدارات محاسبه کننده آنالوگ؛ قسمت سوم

باید هشدار داد که استفاده از تکنیک های حسابان برای استخراج یک کمیت از کمیت دیگر محدودیتهای خاص خود را دارد. مشتق گیری تمایل نامطلوبی برای تقویت "نویز" موجود در متغیر اندازه گیری شده دارد، چرا که نویز معمولاً با فرکانس هایی بسیار بیشتر از فرکانس متغیر اندازه گیری شده ظاهر می شود و فرکانس های بالاتر به دلیل ماهیت خود دارای نرخ تغییر بالاتری در طول زمان هستند. 

برای نشان دادن این مشکل، فرض کنید که ما از سیگنال سرعت به دست آمده از یک تاکوژناتور ذغالی، برای اندازه گیری شتاب یک خودرو استفاده کنیم. اتصال ضعیف ذغالها یک سری افتهای لحظه ای در ولتاژ خروجی تاکوژنراتور ایجاد می کنند و مشتق گیر متصل به آن، این افتها را به عنوان تغییرات بسیار سریع سرعت تفسیر می کند. برای خودرویی که با سرعت ثابت حرکت می کند، و نه شتاب افزاینده یا کاهنده دارد، سیگنال شتاب باید 0 ولت باشد ، اما "نویز" ناشی از یک تاکوژنراتور معیوب باعث می شود در سیگنال مشتق گیری شده دارای نیزه هایی باشیم که به صورت اشتباه دوره های کوتاه افزایش یا کاهش سرعت را نشان می دهد. 

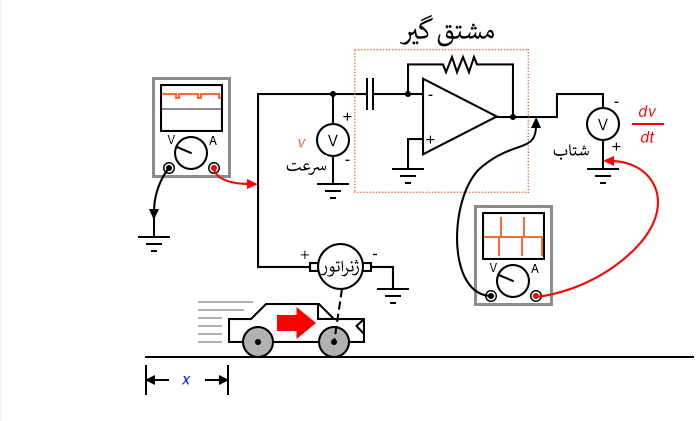
لازم نیست که دامنه ولتاژ نویز موجود در سیگنال مشتق گیری شده خیلی زیاد باشد تا مشکل ایجاد کند. تنها چیزی که لازم است این است که شکل موج نویز افزایش یا کاهش سریعی داشته باشد. به عبارت دیگر، هر نویز الکتریکی با مؤلفه dv/dt زیاد هنگام مشتق گیری مشکل ساز خواهدشد حتی اگر دامنه کمی داشته باشد. 

لازم به ذکر است که مشکل خطای ویژه مدارهای اندازه گیری/محاسباتی ناشی از طبیعت مدارات آنالوگ نیست، بلکه بیشتر ناشی از ذات فرآیند مشتق گیری است. مهم نیست که چگونه مشتق گیری کنیم، "نویز" در سیگنال سرعت همواره سیگنال خروجی را خراب می کند. مطمئناً، اگر از یک سیگنال دو بار مشتق بگیریم، همانطور که برای دستیابی به سرعت و شتاب از سیگنال موقعیت عمل کردیم، نویز تقویت شده توسط مدار مشتق گیر اول دوباره توسط مشتق گیر بعدی تقویت می شود، بنابراین دارای یک مسئله ی ترکیبی می شویم. 

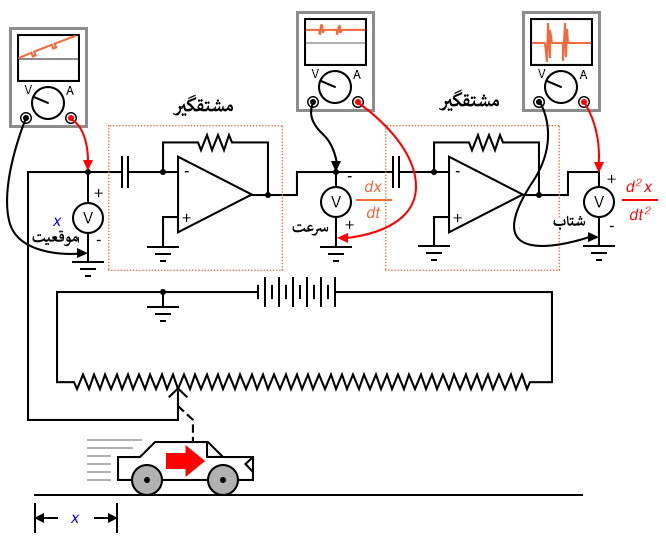
انتگرال گیری چنین مشکلی ندارد، زیرا انتگرال گیرها همانند یک فیلتر پایین گذر عمل می کنند و سیگنال های ورودی با فرکانس بالا را کاهش می دهند. در واقع ، تمام قله های بالا و پایین ناشی از نویز سیگنال با گذشت زمان همدیگر را خنثی می کنند تا نتیجه حاصل کاهش یابد. بنابراین ممکن است تصور شود که ما می توانیم با اندازه گیری مستقیم شتاب و انتگرال گیری از آن برای بدست آوردن سرعت، از این مشکلات پرهیز کنیم. در واقع، محاسبه را به صورت "معکوس" روشی که قبلا نشان داده شد پیش ببریم. 

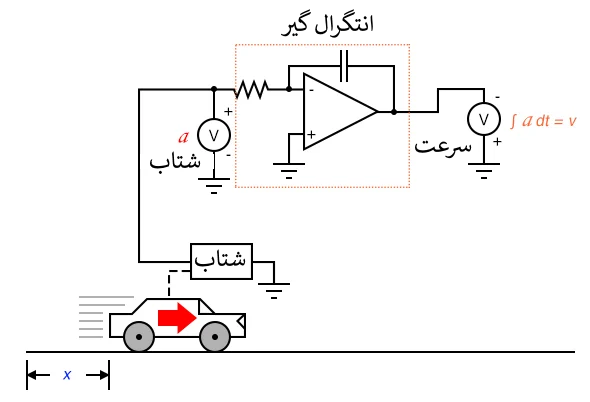
متأسفانه، پیروی از این روش ممکن است ما را به سوی مشکلات دیگری سوق دهد، که یکی از آنها اشکالی رایج در انتگرال گیرهای آنالوگ معروف به رانش (drift) است. همه تقویت کننده های عملیاتی مقداری جریان بایاس ورودی دارند و این جریان تمایل دارد تا به همراه بار ناشی از سیگنال ولتاژ ورودی در خازن ذخیره شود. به عبارت دیگر، انتگرال گیرهای آنالوگ از گرایش ولتاژ خروجی شان به سوی رانش رنج می برند حتی اگر هیچ ولتاژی در ورودی نداشته باشند و در نتیجه در طول زمان دارای یک خطای تجمعی هستند. البته خازن های غیر ایده آل به دلیل مقاومت داخلی تمایل دارند تا بار ذخیره شده در خود را با گذشت زمان از دست بدهند و در نتیجه جابجایی ولتاژ خروجی به سمت صفر می رود. این مشکلات ناشی از طبیعت مدارهای آنالوگ است و ممکن است با استفاده از مدارات محاسباتی دیجیتال برطرف شوند. 

با وجود اشکالات مداری، خطاهای احتمالی ممکن است ناشی از انتگرال گیری یک کمیت (مانند شتاب) برای بدست آوردن کمیت دیگر (مانند سرعت) باشد، چرا که انتگرال گیرهای این گونه کار می کنند. اگر نقطه "صفر" سنسور سیگنال اولیه به صورت ایده آل کالیبره نباشد، حتی در شرایطی که خروجی وجود ندارد، یک سیگنال مثبت یا منفی جزئی تولید می کند. خودروی را در نظر بگیرید که دارای شتاب سنج کالیبره نشده ای غیر ایده آل است، یا شتاب سنجی که تحت تأثیر جاذبه شتاب کمی را بدون وجود شتاب خودرو تشخیص می دهد. حتی با وجود یک انتگرال گیر ایده آل، این خطای حسگر باعث خطای تجمعی در انتگرال گیر می شود، در نتیجه سیگنال خروجی نشانگر تغییر سرعت است در حالی که خودرو نه شتاب می گیرد و نه کند می شود. 

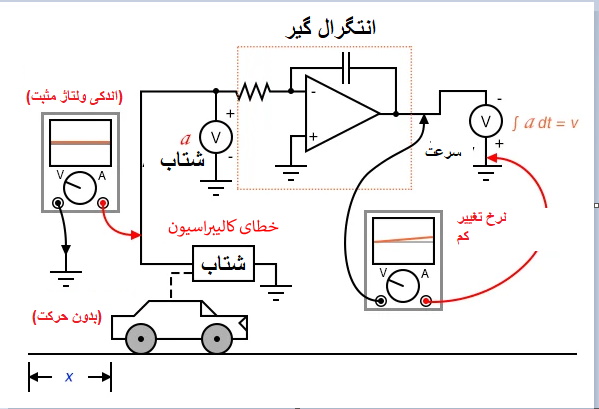
همانند فرایند مشتق گیری، اگر سیگنال انتگرال گیری شده به انتگرال دیگری تغذیه شود، این خطا نیز مرکب خواهد شد زیرا خروجی جابجا شده اولین انتگرال گیر به زودی سیگنال مثبت یا منفی قابل توجهی را برای انتگرال گیر بعدی ایجاد می کند. بنابراین، هنگام انتگرال گیری از سیگنال های حسگر باید دقت شود: اگر سنسور کاملا بر روی "صفر" تنظیم نشده نباشد، خروجی انتگرال گیر جابجا می شود حتی اگر خود انتگرال گیر ایده آل باشد. 

تا کنون، تنها خطاهای انتگرال گیری ناشی از طبیعت مدارها مورد بحث بوده اند: خطاهای ناشی از ایده آل نبودن مدارها و حسگرها. همچنین یک منبع خطای ذاتی ناشی از خود روند انتگرال گیری هم وجود دارد و آن مسئله ثابت ناشناخته است. کسانی که در حساب انتگرال مبتدی هستند نیز می دانند که هر زمان از یک تابع انتگرال گیری بشود، یک ثابت ناشناخته در معادله ظاهر می شود که معمولاً آن را با متغیر C نشان می دهند. درک این عدم قطعیت با مقایسه مشتقات چندین توابع که فقط مقدار ثابت آنها متفاوت است، قابل درک است. 

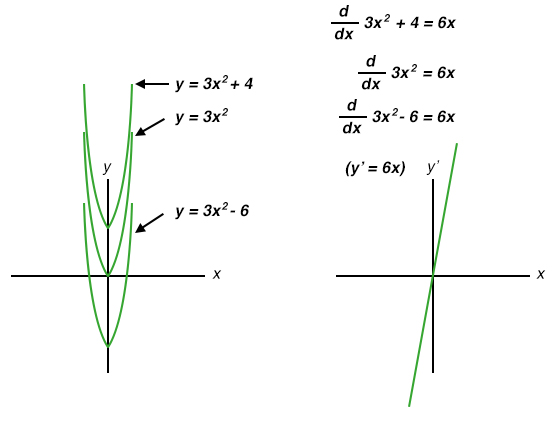
توجه داشته باشید که چگونه هر یک از این سهمی ها (y = 3x2 + C) دارای شکل مشابهی هستند که تنها در مقدار عرض از مبدأ با یکدیگر تفاوت دارند. با این حال ، همه آنها مشتق دقیقاً یکسانی دارند: y'=6x، زیرا همه آنها دارای نرخ تغییر یکسان (شیب) در مقایسه با محور x هستند. گرچه این امر از منظر مشتق گیر کاملاً طبیعی است و انتظار می رود که معادلات مختلف مشتق مشترکی داشته باشند، با این وجود  از دید انتگرال گیر عجیب به نظر می رسند، زیرا چندین پاسخ صحیح برای انتگرال یک تابع وجود دارد. مشتق گیری از یک معادله فقط یک پاسخ دارد، اما انتگرال گیری از همان مشتق برای رسیدن به معادله اصلی ما را به سمت یکسری راه حل های صحیح سوق می دهد. به افتخار این عدم اطمینان، عملکرد نمادین انتگرال گیری را انتگرال نامعین می نامند. 

هنگامی که انتگرال گیر عملیات انتگرال گیری یک سیگنال را نسبت به زمان انجام می دهد، خروجی عبارت است از مجموع سیگنالهای ورودی در طول زمان علاوه بر مقدار اولیه با دامنه دلخواه، که نشان دهنده خروجی قبلی انتگرال گیر در زمان شروع انتگرال گیری است. به عنوان مثال، اگر سرعت یک خودرو در حال حرکت در یک مسیر مستقیم را، که از شهر دور می شود، انتگرال گیری کنم، محاسبه می کنم که سرعت ثابت 50 مایل در ساعت و در مدت زمان 2 ساعت باعث طی مسافت 100 مایل (v.dt∫) می شود، و البته این بدان معنا نیست که خودرو بعد از 2 ساعت 100 مایل با شهر فاصله دارد. تنها چیزی که این نتیجه به ما می گوید این است که خودرو بعد از 2 ساعت رانندگی 100 مایل دورتر از شهر خواهد بود. فاصله واقعی از شهر پس از 2 ساعت رانندگی بستگی به فاصله ابتدایی خودرو از شهر در زمانی دارد که انتگرال گیری آغاز شده است. اگر این مقدار اولیه را برای مسافت ندانیم، پس از 2 ساعت رانندگی نمی توانیم فاصله دقیق خودرو از شهر را تعیین کنیم. 

همین مشکل وقتی ظاهر می شود که از شتاب برای به دست آوردن سرعت، نسبت به زمان، انتگرال گیری کنیم. 

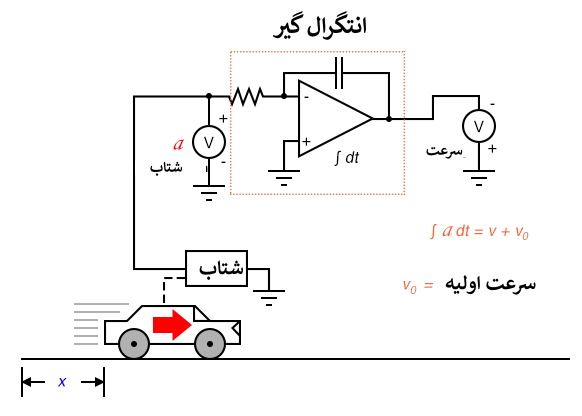
در این انتگرال گیر، سرعت محاسبه شده خودرو فقط در صورتی معتبر خواهد بود که انتگرال گیر هنگام ثابت بودن خودرو (0=v) با مقدار خروجی صفر مقداردهی اولیه شود. در غیر این صورت، انتگرال گیر می تواند هنگام توقف خودرو سیگنال غیر صفر برای سرعت (v0) نشان دهد، زیرا شتاب سنج نمی تواند تفاوت بین یک حالت توقف (0 مایل در ساعت) و یک حالت سرعت ثابت را، مثلا  60 مایل در ساعت، تشخیص دهد. این عدم قطعیت در خروجی انتگرال گیر ذاتی فرایند انتگرال گیری است، نه اینکه ناشی از مدارها یا حسگرها باشد. 

به طور خلاصه، اگر حداکثر دقت برای اندازه گیری کمیتهای فیزیکی مورد نظر است، بهتر است که آن متغیر را مستقیماً اندازه گیری کنید تا اینکه از سایر اندازه گیری ها استخراج کنید. این بدان معنا نیست که مدارات محاسب بی فایده اند. کاملاً برعکس، غالباً محاسبه تنها وسیله عملی برای به دست آوردن اندازه گیری مطلوب است. با این حال ، محدودیتهای مدارات محاسب باید درک شوند و به منظور رسیدن به اندازه گیری های دقیق مورد توجه قرار بگیرند.