چگونه یک کامپیوتر آنالوگ بسازیم؟

Jake Schneider Erik Welsh Brandon Baysinger Parker Jones

مترجم:رضاکیانی موحد

مقدمه

به منظور فهم بهتر دنیای فیزیک، بعضی وقتها لازم است که از مدلهای ریاضی برای پیش بینی عکس العملهای سیستمهای فیزیکی ،مانند وزنه ای که در انتهای یک فنر نوسان می کند، استفاده کنیم. به خاطر استفاده از معادلات دیفرانسیل، ممکن است که رفتار یک مدل این چنین را دقیقا مدلسازی کرد. به هرحال، دیدن پاسخهای گرافیکی جواب چنین مدلهایی پیچیده است. کامپیوترهای آنالوک به دلیل استفاده از ضرب کننده ها، جمع کننده ها و انتگرال گیرها می توانند به سرعت و با دقت پاسخ معادلات دیفرانسیل را ترسیم کنند.

خلاصه

به منظور مدل سازی نیروها، نوسان میرای یک وزنه ی آویخته به یک فنر ما یک کامپیوتر آنالوک با استفاده از جمع کننده و انتگرال گیر ساخته ایم تا با حل معادله دیفرانسیل زیر:

بتوانیم پاسخ سیستم را به موجهای سینوسی، مثلثی و مربعی در فرکانسهایی بین 2 تا 2 مگاهرتز تعیین کنیم. برای ساخت این کامپیوتر دو مدار را طراحی کرده ایم. هر دو مدار معادله ی دیفرانسیل یکسانی را حل می کنند اما مدار دوم بسیار بهتر از مدار اول است.

بررسی ریاضی

مدلسازی حرکت میرای یک سیستم فنر-وزنه بر حل معادله ی دیفرانسیل زیر استوار است:

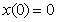
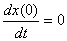
که در این معادله M وزن وزنه ی متصل شده به فنر، K_d ثابت میرایی، K_s ثابت فنر و F(t) نیروی وارد شده می باشد. به منظور حل این معادله ابتدا باید معادله ی همگن حل شود تا پاسخ های طبیعی سیستم بدست آیند. حل معادله ی همگن به دست می دهد:

پس از آن باید به دنبال جوابهای خاص معادله ی اصلی بگردیم. با استفاده از تبدیل لاپلاس معادله را برای بدست آوردن x_L(s) حل می کنیم:

و با تبدیل لاپلاس معکوس می توانیم به x(t) برسیم. با حل این انتگرال پاسخ معادله ی دیفرانسیل مدلسازی فنر-وزنه به دست می آید:

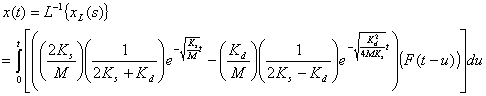
یا می توان از یک کامپیوتر آنالوگ برای رسیدن به جواب استفاده کرد.

انتگرال گیر

یکی از مشکلاتی که قبل از ساختن هر مداری با آن مواجه می شویم روش ساخت یک انتگرال گیر قابل اعتماد است. در ابتدا ما سعی کردیم تا از یک خازن برای فیدبک انگرال گیر استفاده کنیم. انتگرال گیر شامل یک مقاومت ورودی (10 کیلو تا 1 مگا اهم)، و یک خازن فیدبک (0.1 میکروفاراد) و یک تقویت کننده ی عملیاتی LM741 می باشد. در این مورد، انتگرال گیر خروجی را با نسبت -1/RCs ورودی تقسیم می کند (s فرکانس ورودی است). یکی از مشکلات چنین انتگرال گیری عدم توانایی آن در نگه داشتن یک شکل موج برای بیشتر از یک زمان مشخص است. انتگرال گیر شکل موج را هنگامی که یک موج مربعی به ورودی اعمال شود بیشتر نگه می دارد تا زمانی که ورودی سینوسی باشد. همچنین، مقاومت بیشتر در ورودی سبب می شود که انتگرال گیر بیشتر شکل موج را نگه دارد. مداری این چنین دارای یک خازن 0.1 میکروفاراد و یک مقاومت ورودی 1 مگااهم است. این مدار می تواند شکل موجهای زیر را برای زمانهای زیر نگه دارد:

شکل موج	زمان نگهداری(ثانیه)
مربعی	47
مثلثی	18
سینوسی	10

(فرکانس تمام موج ها 130 هرتز است)

انتگرال گیر نمی تواند شکل موج را نگه دارد چرا که فانکشن ژنراتور ما برای هیچ کدام از سیگنالها خروجی صفر نداشت. اگر این طور نبود انتگرال گیر ما بهتر عمل می کرد.

از این رو، ما سعی کردیم یک مدار بهتر بسازیم و آن را انتگرال گیر با فیدبک موازی نامیدیم. این مدار دارای یک مقاومت موازی با خازن فیدبک بود. شکل موج خروجی بسیار پایدارتر بود. بدین منظور ما از یک مقاومت 10مگااهم به عنوان ورودی و از یک مقاومت 5.1 مگااهم به موازات خازن 0.1 میکروفاراد استفاده کردیم. در نتیجه تابع انتقال تبدیل شد به

 -R_F / (R_F*R*C*s + R)

که در این تابع R_F مقاومت فیدبک و R مقاومت ورودی است:

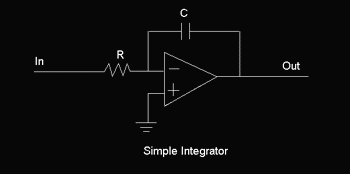
انتگرال گیر ساده

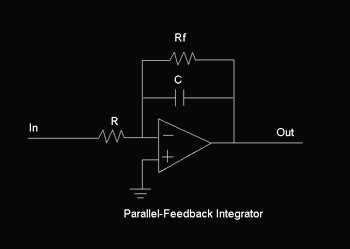
انتگرال گیر با مقاومت در فیدبک

با به دست آوردن یک مدار پایدار، مدلسازی معادله را با مدارات بزرگتر دنبال کردیم.

طراحی اولین کامپیوتر

ما در اولین طرح خود سعی کردیم که مستقیما از مداری که داشتیم ،بدون کوچک کردن آن، استفاده کنیم. دراینجا بلوک دیاگرام مدار آمده است:

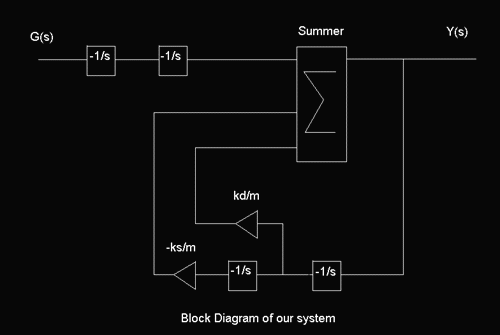
و در اینجا نقشه ی مدار ساخته شده را می بینید:

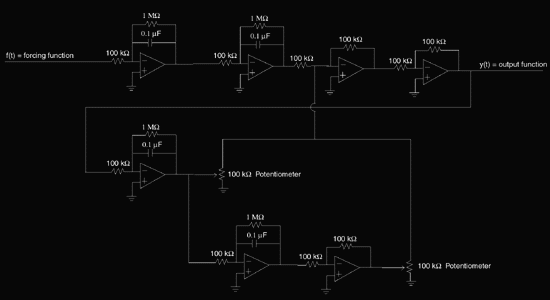
زمانی که این مدار را ساختیم با اشکالات چندی مواجه شدیم که ما را به ساده تر کردن مدار هدایت کرد. بزرگترین مسئله به خاطر تعداد زیاد تقویت کننده های عملیاتی بود که مدار را مستعد نویز کرده بود. هر جزء مدار به صورت جداگانه نویز زیادی نداشت اما در کنار هم میزان نویز تقویت شده توسط هر جزء مدار بیشتر و بیشتر می شد. همچنین این نویز سبب می شد تا ایجاد یک شکل موج پایدار با مشکل مواجه شود. آفست دی.سی فانکشن ژنراتور باید برای هر شکل موج ورودی به صورت جداگانه تنظیم شود تا خروجی پایدار شود. اگر آفست دی.سی حتی مقدار اندکی از مقدار مورد نیاز منحرف شود خروجی به سرعت تبدیل به یک مقدار دی.سی تبدیل می شود.

به خاطر تأثیر زاید نویز (همانطور که در بخش بعدی خواهیم گفت) تصمیم گرفتیم تا مدار را خلاصه کنیم.

پاسخ مدار اصلی به ورودی های گوناگون

تمام شکل موج های ورودی زیر با دامنه و فرکانس یکسان (100 هرتز) به مدار اعمال شده اند. در تمام دیاگرامهای زیر ورودی با رنگ آبی و خروجی با رنگ سبز مشخص شده اند:

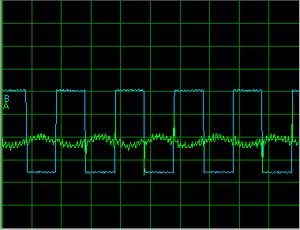
موج مربعی

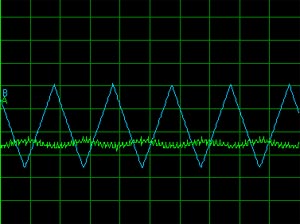
موج مثلثی

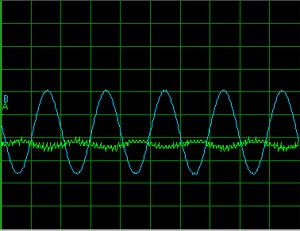
موج سینوسی

توجه کنید که در تمامی خروجی ها اثرات نویز به خوبی قابل مشاهده است. تمام شکل موجهای خروجی نوسانهای مشخص ناشی از نویز را نشان می دهند. همچنین می توان توجه کرد که شکل موج های خروجی ،فارغ از ورودی اعمال شده، بسیار شبیه هستند. همچنین این مدار پاسخ بزرگتری ،دست کم در دامنه، برای موج مربعی نسبت به موج سینوسی یا مثلثی دارد.

طرح کامپیوتر دوم

پس از تحقیق و کار عملی مدار خلاصه شده ی کامپیوتر تهیه شد. به جای استفاده از جمع کننده ها، تقویت کننده و انتگرال گیرهای جداگانه از جمع کننده-انتگرال گیر استفاده کردیم. این امر اجازه داد تا تعداد زیادی از عناصر را حذف کنیم. در اینجا بلوک دیاگرام مدار دومی که ساختیم را می بینید:

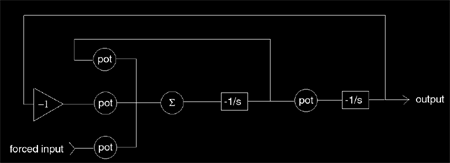
در زیر مدار ساخته شده را می بینید. توجه کنید که تعداد عناصر مدار چقدرکمتر شده اند. بنابراین امکان وارد شدن نویز به مدار کمتر شده است.

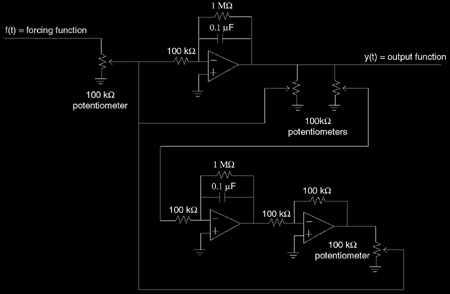
در این مدار از 3 تقویت کننده ی عملیاتی استفاده شده است. 2 تقویت کننده برای انتگرال گیری و جمع و یکی به عنوان معکوس کننده استفاده شده اند. ثابتهای معادله ی دیفرانسیل مدل شده نمی توانند به صورت مجزا تنظیم شوند. در عوض، 4 پتانسیومتر اجازه می دهند که نسبتهای بین آنها تنظیم شود.

این مدار پاسخ بهتری نسبت به ورودی اعمال شده دارد. با این مدار مشکل نویز در مدار قبلی حل شده است. همچنین، ناچار نیستیم تا آفست دی.سی فانکشن ژنراتور را برای رسیدن به نتیجه تنظیم کنیم. با روشن کردن مدار بلافاصله شکل موج خروجی ظاهر می شود.

پاسخ مدار دوم به شکل موجهای ورودی

در زیر شکل موجهای ورودی با رنگ سبز و خروجی ها با رنگ آبی نمایش داده شده اند:

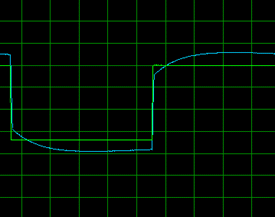
موج مربعی 1 هرتز

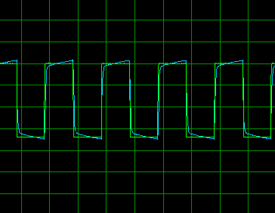
موج مربعی 10 هرتز

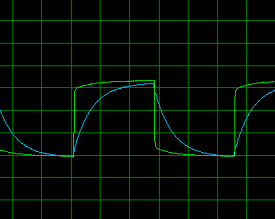
موج مربعی 100 هرتز

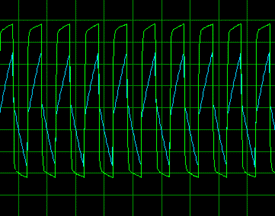
موج مربعی 1000 هرتز

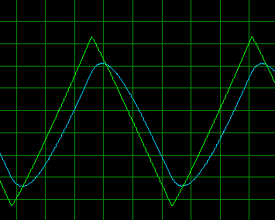
موج مثلثی 100 هرتز

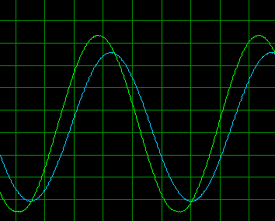
موج سینوسی 100 هرتز

اثرات نویز به مقدار زیادی کم شده اند. شکل موج خروجی دیگر نوسان آنچنانی (مانند مدار اول) ندارد. توجه کنید که چگونه شکل موج خروجی در هر مورد سعی می کند که (بر خلاف مدار اول) شکل موج ورودی را به خود بگیرد. همچنین به شیفت فازی بوجود آمده در مورد ورودی های سینوسی و مثلثی توجه کنید.

بحث

خروجی مدار اول آنچنان که انتظار داشتیم نبود. توجه کنید که ورودی های زیادی برای اعمال نویز به مدار وجود داشت و خروجی به شدت از نویز تأثیر گرفته بود. شکل موج های خورجی خیلی بزرگ نبودند و در اثر نویز اعوجاج داشتند.

درباره ی شکل موجهای خروجی مدار دوم می توان بیشتر بحث کرد. خروجی سعی می کرد که شکل موج ورودی را به خود بگیرد. این امر در فرکانس 1 هرتز با موج مربعی بیشتر قابل توجه است. توجه کنید که چگونه شکل موج خروجی نمی تواند کاملا با شکل موج ورودی هماهنگ شود. هنگامی که موجهای سینوسی و مثلثی به مدار اعمال شوند این عدم توانایی با تغییر فاز نسبت به ورودی خود را نشان می دهد. در هر مورد، با افزایش فرکانس تأثیر تغییر فاز بر روی خروجی افزایش می یابد. کامپیوتری که ما از آن برای ترسیم شکلها استفاده کردیم نمی توانست با سرعت کافی نمونه برداری کند اما عکس العمل مدار در برابر فرکانس 2 مگاهرتز مربعی واقعا جالب توجه بود. در این فرکانس خروجی فانکشن ژنراتور کاملا اعوجاج داشت. جالب است که در خروجی نیز اعوجاج زیادی دیده می شود که ناشی از این است که مدار سعی می کند تا خود را با ورودی مطابقت دهد.

تغییر فاز و عدم توانایی تطابق با ورودی را می توان با روشهای گوناگونی تشریح کرد. در دنیای فیزیک می توان این شیفت را به عنوان اینرسی وزنه ی آویخته شده به فنر محسوب کرد. با تغییر مقدار ورودی وزنه نمی تواند همزمان تغییر وضعیت بدهد. به خاطر اینرسی وزنه ابتدا باید حرکت خود را به انتها برساند و پس از در جهت دیگر حرکت کند. در نظریه ی سیستمها این تغییر فاز به سادگی ناشی از مدار است. مدار کاملا خطی نیست و این امر اختلالی در هر شکل موج ورودی که اعمال شود ایجاد می کند.

نتیجه گیری

پس از تنظیم مدار فهمیدیم که یک کامپیوتر آنالوک راه حل مؤثری برای حل معادلات دیفرانسیل ارائه می دهد. کامپیوترهای آنالوگ دقتی مشابه کامپیوترهای دیجیتال ندارند اما برای حل معادلات دیفرانسیل به صورت غیرقابل باوری سریع هستند. به خاطر اینکه کامپیوترهای آنالوگ تمام معادله را در یک لحظه حل می کنند ما می توانیم فرکانس یا شکل موج تابع نیرو را عوض کنید و بدون تأخیر پاسخ را ببینیم. به هرحال، این کامپیوترها چند نقطه ضعف هم دارند. تنظیم شرایط اولیه ی یک معادله ی دیفرانسیل برای آنها سخت است چرا که به یک منبع ولتاژ شناور که بتواند به سرعت از مدار جداشود نیاز دارد. همچنین، صفر کردن آفست دی.سی خروجی به وسیله ی فانکشن ژنراتور مشکل زاست. در انتها، کامپیوترهای آنالوگ راه مؤثری برای حل کردن یک مدل فیزیکی واقعی هستند.

 منبع

https://www.clear.rice.edu/elec301/Projects99/anlgcomp/