برق-قدرت
اینجا فقط از برق و الکترونیک و کامپیوتر حرف می زنیم
برق-قدرت
اینجا فقط از برق و الکترونیک و کامپیوتر حرف می زنیمطراحی آسانسور با رویکرد دیجیتال، قسمت سوم

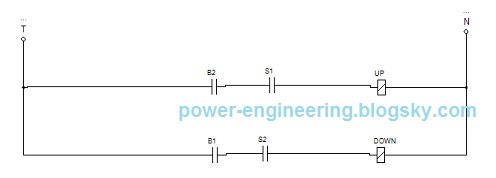
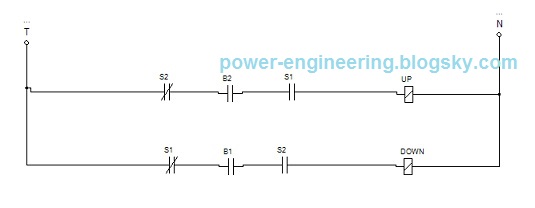
در قسمت قبلی گفتیم که مدار فرمان نهایی آسانسور برای یه ساختمون سه طبقه می شه به شکل زیر:
به زبون دیجیتال اگه بخواهیم بنویسیم داریم:
up=(s1.(b2+b3))+(s2.upp.(b1+b3))
down=(s3.(b1+b2))+(s2.downn.(b1+b3))
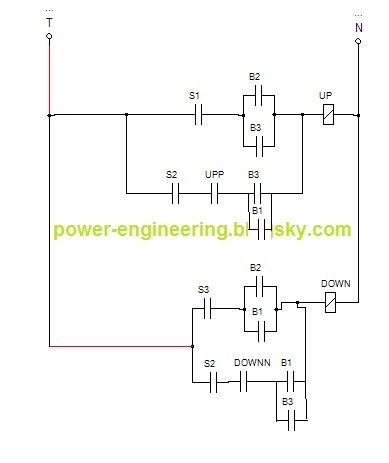
حالا ببینم که اگه همین مدار فرمانو بخواهیم به صورت دیجیتالی و با مدار فرمان طراحی کنیم سر از کجا در میاریم.
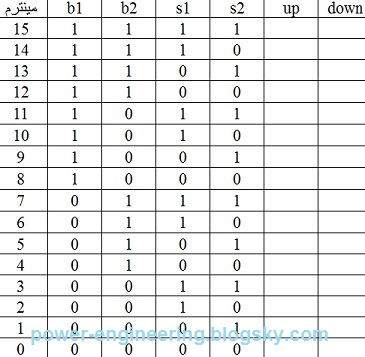
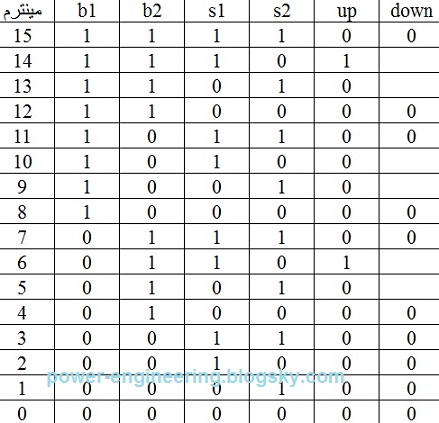
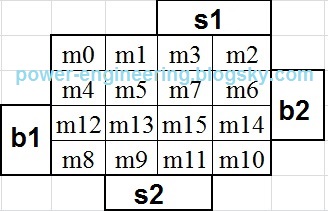
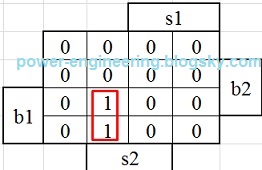
تعداد متغیرها رو اول باس بشمریم. سه تا سوئیچ s و سه تا پوش باتون b و دو تا کنتاکتور upp و downn میشه به عبارتی 8 تا متغیر. تعداد حالتهای مختلف 8 متغیر میشه 256 حالت. حتی اگر یه جدول با 256 سطر رو بکشید و تحلیل کنیم ساده کردن اون کار حضرت فیله. برای ساده کردن مسئله میاییم و دو گوله رو به کار می ندازیم. می دونیم که سوئیچهای s همواره و همواره فقط یکی شون وصل هست و دو تای دیگه خاموش هستن. با این شرط منطقی میاییم و تنها وصل بودن یکی رو همراه با اون 5 تا متغیر باقیمونده جدول می کنیم. فقط نکته ای که هست اینه که در طبقات اول و سوم متغیرها از 5 به 3 کاهش داده میشه چون کنتاکتورهای upp یا downn در این طبقات ریست می شن و ارزش اونها صفر هست. اول کار بریم سراغ طبقه ی اول. نمودار متغیرهاش به صورت زیر هستش:

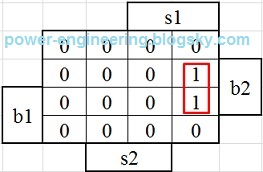
همون طور که دیده میشه ستون down صفر هست و ستون up در مینترمهایی که b2 یا b3( یا هر دو) فشار داده شده باشن برابر با یک هست. خلاصه ی جدول برای خروجی up به صورت زیر در میادش:
که معنی ش میشه:
up=s1.b2+s1.b3=s1.(b2+b3)
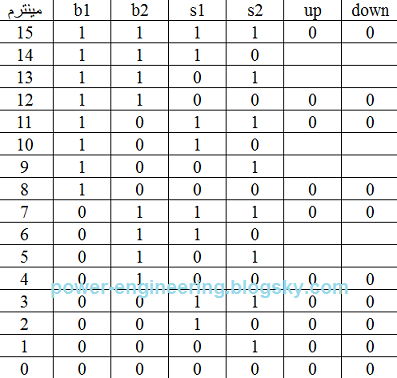
حالا فرض کنیم آسانسور در طبقه ی سوم هستش. بازهم تنها متغیرهایی که در نظر می گیریم s3 هست به همراه پوش باتونها. جدول خروجیها به صورت زیر هستش:
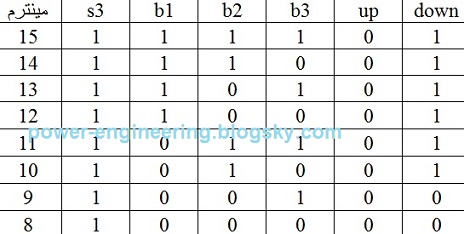
ستون خروجی up همه ی مینترماش صفره و ستون downn هر جا که b1 یا b2 (یا هر دو تاش) فشرده شده باشن برابر با یک هستش.جدول خروجی down میشه: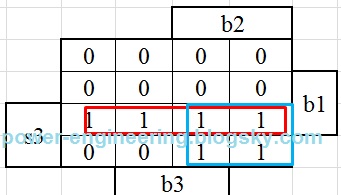
که معنی ش میشه:
down=s3.b1+s3.b2=s3.(b1+b2)
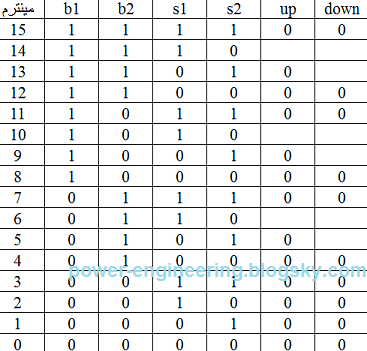
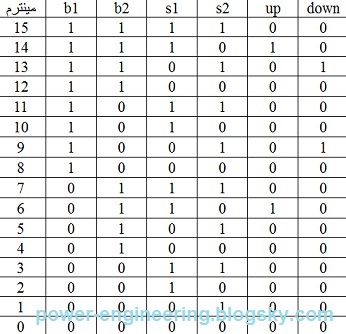
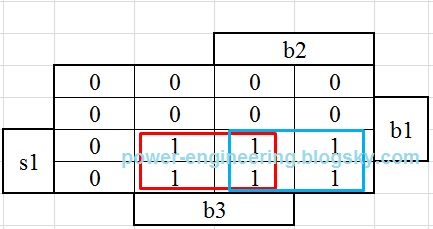
قضیه برای وقتی که آسانسور توی طبقه ی دوم ایستاده پیچیده تره. اگه آسانسور از پایین اومده باشه بالا پس upp فعال هست و باید ارزش منطقی اون رو برابر با 1 بگیریم. از طرف دیگه اگه آسانسور از طبقه ی سوم پایین اومده باشه پس downn فعال هستش و باید ارزش منطقی اون رو برابر با 1 بگیریم. از طرف دیگه می دونیم که upp و downn با همدیگه فعال نمیشن. پس به جای یه جدول بزرگ دو تا جدول کوچیک تشکیل می دیم. یه بار برای وقتی که upp=1 و دفعه ی بعدی برای وقتی که downn=1. بعد نتیجه ی حاصل رو با نتایجی که در بالا به دست آوردیم جمع می کنیم. جدول درستی خروجیها برای وقتی که upp=1 به صورت زیر هستش:
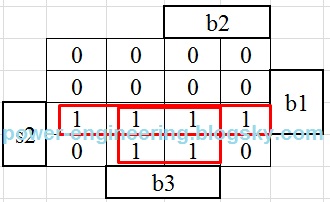
به مینترم های12ام و 14ام توجه کنید. درسته کهb1 فشرده شده اما همون طور که در قسمت دوم گفتیم در این وضعیت اتاقک آسانسور باید به حرکت خودش به سمت بالا ادامه بده و بعد برگرده پایین، پس در نتیجه خروجی upp برابر با 1شده. در نتیجه خروجی up میشه:
up=s2.upp.(b1+b3)
توجه کنید که چون فرض کردیم upp=1 باید upp رو در نتیجه ضرب بکنیم.
حالا میریم سراغ وضعیتی که downn=1 هستش:
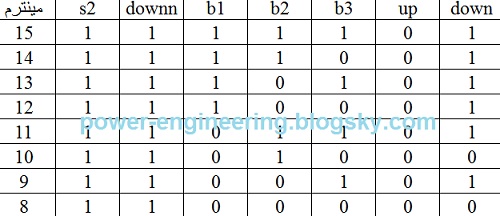
بازهم در مینترمهای 9ام و 11ام با اینکه پوش باتون b3 فشرده شده آسانسور میره پایین و علتش رو هم که در قسمت قبلی توضیح دادیم. نتیجه ی خروجی down میشه:

همون طور که می بینید این جدول با جدول خروجی up مو نمیزنه جز اینکه در اون مورد باید upp رو ضرب می کردیم و حالا باید downn رو ضرب کنیم. پس خروجی میشه:
down=s2.downn.(b1+b3)
در نهایت باید خروجی های به دست اومده از این چار تا جدول رو با هم جمع بزنیم. در نتیجه داریم:
up=(s1.(b2+b3))+(s2.upp.(b1+b3))
down=(s3.(b1+b2))+(s2.downn.(b1+b3))
یعنی دقیقا به همون نتیجه ای رسیدیم که از تحلیل مدار به دست آوردیم. اگر هم بخواهیم که این مدار رو به صورت لدر طراحی کنیم حاصل اون همون شکل اول هست. پس نتیجه می گیریم که با استفاده از ساده سازی مدار منطقی میتونیم به همون نتیجه ای برسیم که از طراحی عادی مدار فرمان به دست میادش.
اگه حوصله ای بود این بحث رو با مدار فرمان آسانسور چهار طبقه ادامه میدیم و داستان رو جمع ش می کنیم.
طراحی آسانسور با رویکرد دیجیتال، قسمت اول

عموما کسی که می خواد یه مدار فرمان طراحی کنه اول از پروسه ی مورد نظرش سوال می کنه، بعد که چم و خم کار رو بررسی کردشروع می کنه به طراحی مدار فرمان. بیشتر کار هم به صورت شهودی و بر اساس تجربه صورت می گیره. من در یک سلسله پست (که احتمالا 4 یا 5 قسمت بشه) می خوام طراحی شهودی رو با طراحی دیجیتال مقایسه کنم تا ببینم اگه از اول بر اساس یه مدار منطقی بریم جلو چقدر میتونیم به طراحی یه مدار فرمان خوب نزدیک بشیم.
برای مثال از طراحی آسانسور شروع می کنیم. مدار فرمان آسانسور مدار فرمان نسبتا پیچیده ای هست و به همین دلیل یه قسمتهایی از مدارات رو حذف می کنم تا از هدف اصلی این بحث خیلی دور نیفتم. پس:
- آسانسور ما در هر طبقه دارای یه سنسور هست که نشون دهنده ی وارد شدن آسانسور به طبقاته. از وقتی که آسانسور وارد یه طبقه بشه تا زمانی که به صورت کامل درون اون طبقه قرار بگیره (یعنی در اتاقک آسانسور روبروی در هر طبقه قرار بگیره) اتفاقی نمیافته. وقتی که اتاقک آسانسور کاملا روبروی در خروجی قرار گرفت اون وقته که سنسور اون طبقه فعال می شه. منظورم اینه که ما حالتی نداریم که هیچ یکی از سنسورهای طبقات فعال نباشند و مثلا اتاقک آسانسور بین طبقات باشه. پس یا آسانسور در طبقه اول هست یا دوم یا سوم و ...... اسم این سنسورهای رو میذارم کلید s. فرض می کنیم که این کلیدها همه شون نورمالی اوپن هستند. یعنی وقتی اتاقک آسانسور به یه طبقه برسه سنسورش بسته میشه و وقتی از اون طبقه خارج بشه سنسورش باز میشه.
- برای هر طبقه یه پوش باتون در بیرون اتاقک آسانسور و روی دیوار قرار داره که با فشار دادن اون پوش باتون، اتاقک آسانسور باید در اون طبق توقف بکنه. چون وقتی که پوش باتون ول بشه اطلاعات از بین میره ، پوش باتون رو به یه کنتاکتور وصل می کنیم و از کنتاکتهای اون کنتاکتور استفاده می کنیم به جای خود اون پوش باتون.هر کنتاکتوری برای وصل ماندن از کنتاکت نگه دارنده ی خودش استفاده می کنه. اسم پوش باتونها و کنتاکتورها رو گذاشتمb. به ازای هر پوش باتون در بیرون آسانسور یکی هم داخل خود اتاقک آسانسور هست که موازی با پوش باتون بیرون اتاقک هست ولی من برای ساده تر شدن نقشه اون رو حذفش کردم.
- مدار فرمان آسانسور سه تا فرمان کلی داره: بالا، پایین و توقف. این فرمانها اعمال میشن به یه مدار قدرت چپگرد-راستگرد معمولی که نقشه ش رو میتونید از هر جایی بردارید. یه نمونه ش اینجاست. وقتی که پوش باتون یه طبقه زده بشه اتاقک آسانسور حرکت می کنه تا برسه به اون طبقه. در اونجا سنسور طبقه فعال میشه و فرمان قطع حرکت رو صادر می کنه که در نتیجه باید کنتاکتورهای چپگرد-راستگرد هر دو غیر فعال بشن و از کار بیفتن.