
برق-قدرت
اینجا فقط از برق و الکترونیک و کامپیوتر حرف می زنیم
برق-قدرت
اینجا فقط از برق و الکترونیک و کامپیوتر حرف می زنیمطراحی آسانسور با رویکرد دیجیتال، قسمت ششم

دو تا پیچ اصلی در طراحی مدار فرمان برای آسانسور ساختمون چار طبقه رو رد کردیم و مونده دو تا پیچ دیگه: طراحی مدار فرمان وقتی که اتاقک آسانسور توی طبقه ی دومه و وقتی که توی طبقه ی سومه.
باز دوباره جدول صحت خروجی ها رو میکشیم ولی باید یادمون باشه که بر خلاف دو تا مدار قبلی (قسمت پنجم) اینبار کنتاکتورهای upp و downn روشن هستند و باید در جدول بیان. فقط چون هر کدوم روشن باشه اون یکی خاموشه میتونیم جدول رو ساده ش کنیم و یه بار برای upp=1 بنویسیم و یه بارم برای downn=1. دست آخر هم باید یادمه باشه که کنتاکتهای باز s2 و upp (یا down) رو باید در مدار طراحی شده سری بکنیم:
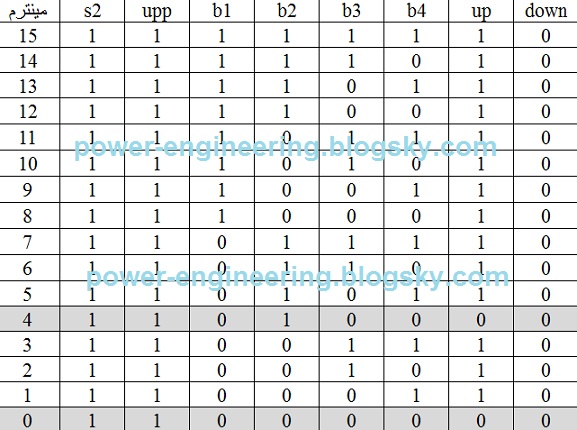
همون طور که دیده میشه وقتی که کلیدهای طبقات مختلف رو می زنیم فقط در مینترهای 4ام و 0ام هست که آسانسور حرکتی نمی کنه. در بقیه ی موارد اتاقک آسانسور باید بره بالا چون upp=1( اینکه چرا باید بره بالا رو قبلا مفصل توضیح ش دادیم). پیاده کردن جدول به صورت زیر در میادش:
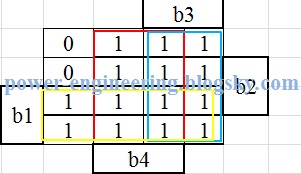
که یعنی:
up=b1+b3+b4
و همون طور که گفتیم باید دو تا ترم دیگه هم ضرب در حاصل جمع بکنیم یعنی:
up=s2.upp.(b1+b3+b4)
برای وقتی که downn=1 هست هم جدول زیر رو داریم:
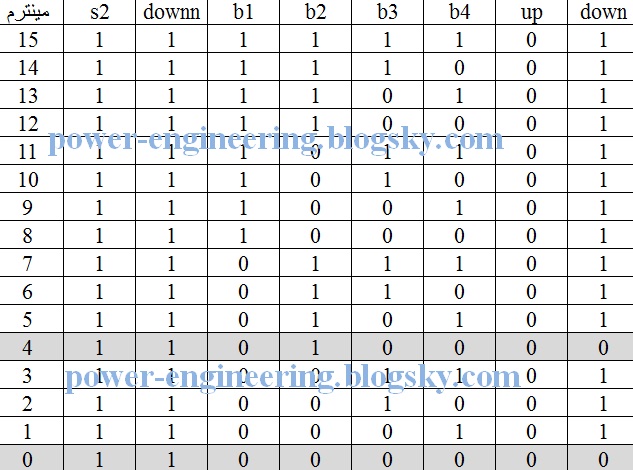
که بازم مینترمهای 4ام و 0ام برابر با صفر هستند و در نتیجه جدول حاصل مساوی جدول بالا می شه. فقط در جدول بالا باید upp رو ضرب می کردیم و حالا باید یادمون باشه که downn رو ضرب کنیم، یعنی :
down=s2.downn.(b1+b3+b4)
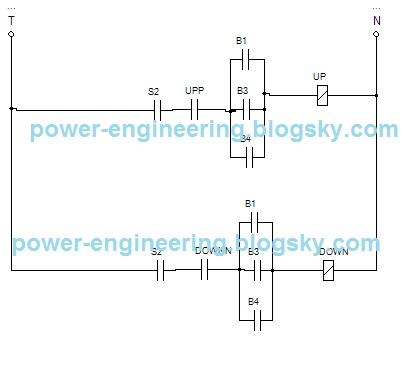
و مدار طراحی شده برای وقتی که اتاقک آسانسور در طبقه ی دومه به شکل زیر در میادش:
حالا بریم سراغ وضعیتی که اتاقک آسانسور در طبقه ی سوم قرار داشته باشه. در این حالت بازهم باید در نظر داشته باشیم که upp یا downn (یکی شون البته) می تونه که روشن باشه و باید در جدول بیادش. پس بازم دو تا جدول درست می کنیم. در حالت اول فرض میکنیم که upp=1 پس داریم:
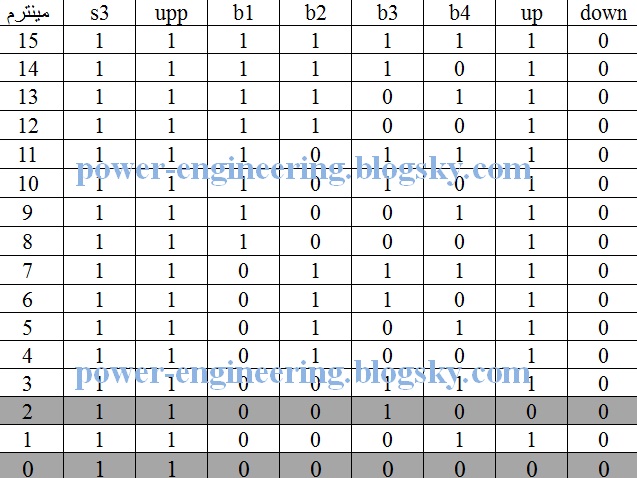
این بار مینترمهای دوم و 0ام برابر با صفر هستند و جدول حاصل برای خروجی up میشه:
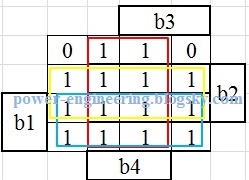
که یعنی :
up=b1+b2+b4
و چون باید تاثیر s3 و upp رو هم در نظر داشته باشیم داریم:
up=s3.upp.(b1+b2+b4)
جدول وضعیت خروجی های وقتی که downn=1 باشه میشه:
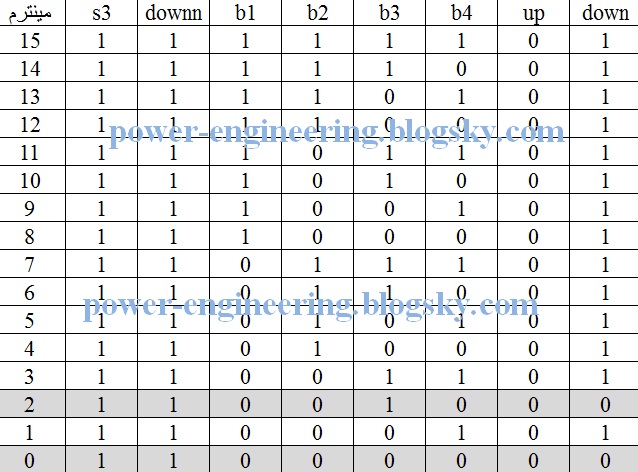
که خلاصه ش میشه دقیقا برابر با جدول قبلی با این تفاوت که اینجا downn=1 هست. پس داریم:
down=s3.downn.(b1+b2+b4)
و نقشه ی مدار فرمان برای وضعیتی که اتاقک آسانسور در طبقه ی سوم هستش میشه:
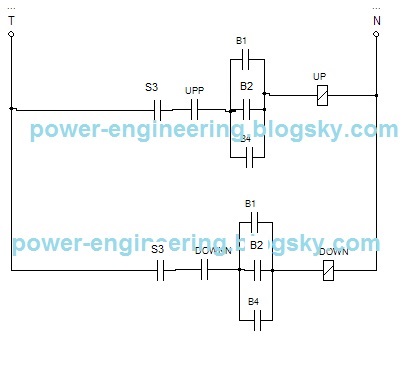
خوب دیگه. کار تمومه. حالا باید بیاییم و قضیه رو جمع ش کنیم. یعنی دو تا نقشه ی این قسمت با نقشه ی قسمت قبل که این هست
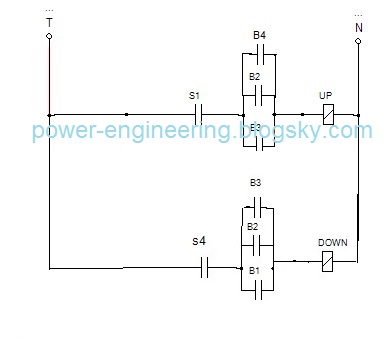
ترکیبشون کنیم توی یه نقشه که دقیقا میشه همون نقشه ی انتهای قسمت چهارم یعنی این:
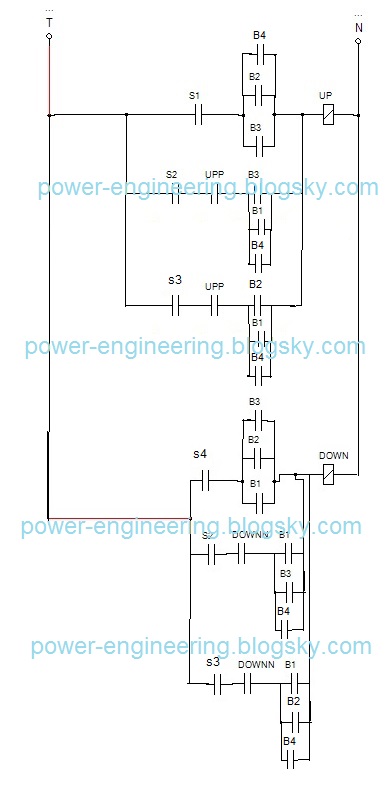
یعنی اگه منطق قضیه رو خوب فهمیده باشید هیچ فرقی نمیکنه که مدارتون رو به صورت معمولی طراحی کنید یا با استفاده از منطق دیجیتال. همین مدار رو البته موقع پیاده سازی می تونید با گیتهای دیجیتالی هم پیاده کنید یعنی کنتاکتهای سری رو به جاشون گیت AND بذارید و کنتاکتهای موازی رو گیت OR و خروجی رو هم بدید به یه رله که اون رله بیادش و کنتاکتورهاتون رو راه اندازی کنه. البته یه سری مسائل و مشکلات هم در زمینه ی نویز و این حرفها خواهید داشت که بهتره کلا قضیه رو بیخیال شید و از همین کنتاکتور و اینها استفاده کنیم.
حالا که منطق قضیه رو خوب فهمیدید دیگه طراحی مدار فرمان برای ساختمان های بلندتر از چار طبقه خیلی سخت نیست. فقط یه کم فشار باس بیارید به مغزتون.
قسمت ششم بحث طراحی مدار فرمان آسانسور در حالی تموم شده که الان فک میکنید دیگه اوستا شدید ولی اشتباه می کنید. ما تا حالا فقط یادتون دادیم که چطور آسانسور رو راهش بندازید. هنوز نگفتیم که وقتی راه افتاد چه طوری باید متوقف ش بکنید. پس ، با ما باشید.
طراحی آسانسور با رویکرد دیجیتال، قسمت پنجم

دیگه وقتشه که بریم سراغ طراحی مدار فرمان ساختمون چارطبقه با تحلیل مدار منطقی. اول از همه میریم سراغ وضعیتی که اتاقک آسانسور در طبقه ی اول قرار گرفته. در این وضعیت هر دو کنتاکتور upp و downn خاموش هستند و نیازی نیست که در جدول صحت ورودیها بیان. فقط s1 رو میاریم و اون هم برابر با 1 هست. جدول دارای 4 متغیر هست و خروجی down هم که البته صفر است. به راحتی یه جدول با 4 متغیر ترسیم می کنیم به شکل زیر:
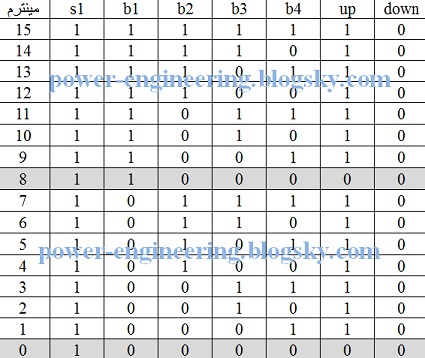
همون طور که میبینیم در مینترمهای 8ام و 0ام خروجی صفر میشه و این وضعیتهایی هست که تنها پوش باتون b1 فشرده شده یا هیچ کدوم از پوش باتونها فشار داده نشدن. جدول ساده شده به صورت زیر درمیادش:
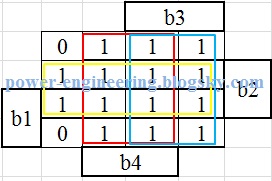
که خلاصه داستان میشه اینکه در هر وضعیتی که یکی از پوش باتونهایذb2، b3 یا b4 فشار داده بشن باید آسانسور بره بالا و به زبان ریاضی:
up=b2+b3+b4
البته چون سوئیچ s1 رو بسته فرض کردیم باید s1 رو هم ضرب در مجموع کنیم و در نتیجه داریم:
up=s1.(b2+b3+b4)
وضعیت آسانسور در طبقه ی چهارم هم به سادگی طبقه ی اول هستش یعنی اینکه:
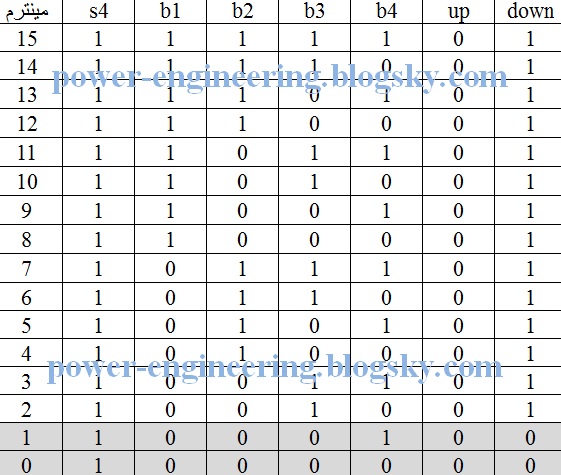
در اینجا دو تا مینترم آخر صفر هستند که یعنی وقتی تنها b4 فشار داده بشه یا هیچ یکی از پوش باتونها فشرده نشن آسانسور نباید حرکت بکنه و در بقیه ی وضعیتهای باید بیادش پایین. به عبارت دیگه:

و به زبان ریاضی این یعنی اینکه:
down=b1+b2+b3
و چون s4 سری شده با مجموع اینها داریم:
down=s4.(b1+b2+b3)
و البته مدار معادل این محاسبات میشه:

تا اینجا ی وضعیت شد طراحی مدار فرمان وقتی که اتاقک آسانسور در طبقات اول یا چهارم هست. می مونه طبقات دوم و سوم که هر وقت فرصت شد بحث رو از همین جا ادامه میدیم.
طراحی آسانسور با رویکرد دیجیتال، قسمت چهارم

دیروز یکی از دوستان زنگ زده و اعتراض کرده که این چه مسخره بازیه؟ میگم چیه داداش؟ میگه من طبقه دوم بودم با خانوم بچه ها. کلید آسانسور رو زدم، آسانسور از طبقه ی اول اومدش بالا. بعد کلیدش رو زدم که دوباره بره طبقه ی اول به جاش رفته طبقه ی سوم و برگشته طبقه ی اول... کلی وقتم گرفته شده. این رو درستش کن.
عارضم خدمت دوستان که میشه درستش کرد. یعنی میشه یه مدار طراحی کنیم که مثلا اگر از طبقه ی اول آسانسور رفتش به طبقه ی دوم بعدبه جای اینکه بره بالا و برگرده طبقه ی اول صاف برگرده پایین. مثلا این مدار:
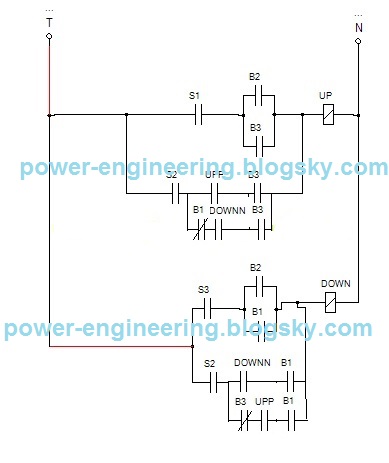
الان در مسیر کنتاکتور down و از بعد از کنتاکت باز s2 ، یه شاخه دیگه بازکردیم که کنتاکت بسته ی b3 توشه و سری شده با کنتاکتهای باز upp و b1. حالا اگر کسی وارد اتاقک آسانسور بشه و پوش باتون b1 رو فشار بده و پوش باتون b3 هم فشار داده نشده باشه، آسانسور به جای اینکه بره بالا و باز برگرده پایین یه راس میره طبقه ی اول.
حالا اشکالش چیه؟
اشکالش اینه که فرض کنیم در یه ساختمان 8 طبقه هستیم و اتاقک آسانسور در طبقه ی چهارم هست. شما در طبقه ی سوم دکمه رو میزنید و خیال دارید برید طبقه ی اول. به محض اینکه وارد آسانسور شدید و خواستید پوش باتون طبقه ی اول رو بزنید اگر یکی مثلا از طبقه ی هفتم کلید رو بزنه آسانسور به جای اینکه بره طبقه ی اول میره طبقه ی هفتم. یعنی همه چی شیر تو شیر میشه و دست آخر معلوم نیست که آسانسور کی به طبقه ی اول برسه. البته میشه برای آسانسور مداری تعریف کرد بر اساس اولویت فشار داده شدن کلیدها و اینکه هر کلیدی که فشار داده بشه اول بره اون طبقه ولی کلا مشکلی حل نمیشه و فقط مدار پیچیده میشه. پس بهتره به جای این جنقولک بازیا از همون مدار ساده ی قبلی استفاده کنیم که در قسمت سوم توضیح دادیمش.
الانم داریم میریم سراغ طراحی مدار فرمان آسانسور برای چار طبقه. اگه این سلسله مطالب رو تا به اینجا با دقت دنبال کرده باشید برای طراحی مدار فرمان به مشکلی بر نمی خوریم. یه شاخه دیگه برای فرمان به مسیر هر یک از کنتاکتورهای up و down اضافه میشه با این تفاوت که در مسیر down دیگه این سوئیچ s4 هست ش که جای s3 رو گیره، به صورت زیر:

اتفاقی که افتاده اینه که در مسیر کنتاکتهای باز s2 یا s3 (یعنی دو طبقه ی وسطی) به جای دو کنتاکت باز موازی سه کنتاکت باز موازی داریم که غیر همنام هستند. یعنی هر یک از کلیدهای سه طبقه ی دیگه که زده بشه فرمان می دهند و بسته به وضعیت کنتاکتورهای upp و downn مسیر بعدی اتاقک آسانسور رو تعیین می کنند. در نهایت مثل مثال قبل آسانسور یه دور کامل میره بالا و بعد یه دور کامل برمیگرده پایین و همین سیکل رو تکرار ش می کنه.
حالا اگه حوصله م گرفت میشینم و جدول صحت ورودی ها رو برای چار طبقه به صورت دیجیتال تحلیل می کنم که خوب البته دو متغیر جدید (یعنی پوش باتون b4 و سوئیچ s4) به مدار اضافه شده اند و حالات ممکن از 256 حالت تبدیل شده اند به 1024 حالت.
طراحی آسانسور با رویکرد دیجیتال، قسمت سوم

در قسمت قبلی گفتیم که مدار فرمان نهایی آسانسور برای یه ساختمون سه طبقه می شه به شکل زیر:
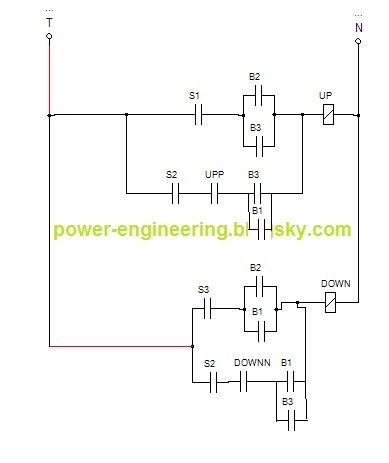
به زبون دیجیتال اگه بخواهیم بنویسیم داریم:
up=(s1.(b2+b3))+(s2.upp.(b1+b3))
down=(s3.(b1+b2))+(s2.downn.(b1+b3))
حالا ببینم که اگه همین مدار فرمانو بخواهیم به صورت دیجیتالی و با مدار فرمان طراحی کنیم سر از کجا در میاریم.
تعداد متغیرها رو اول باس بشمریم. سه تا سوئیچ s و سه تا پوش باتون b و دو تا کنتاکتور upp و downn میشه به عبارتی 8 تا متغیر. تعداد حالتهای مختلف 8 متغیر میشه 256 حالت. حتی اگر یه جدول با 256 سطر رو بکشید و تحلیل کنیم ساده کردن اون کار حضرت فیله. برای ساده کردن مسئله میاییم و دو گوله رو به کار می ندازیم. می دونیم که سوئیچهای s همواره و همواره فقط یکی شون وصل هست و دو تای دیگه خاموش هستن. با این شرط منطقی میاییم و تنها وصل بودن یکی رو همراه با اون 5 تا متغیر باقیمونده جدول می کنیم. فقط نکته ای که هست اینه که در طبقات اول و سوم متغیرها از 5 به 3 کاهش داده میشه چون کنتاکتورهای upp یا downn در این طبقات ریست می شن و ارزش اونها صفر هست. اول کار بریم سراغ طبقه ی اول. نمودار متغیرهاش به صورت زیر هستش:

همون طور که دیده میشه ستون down صفر هست و ستون up در مینترمهایی که b2 یا b3( یا هر دو) فشار داده شده باشن برابر با یک هست. خلاصه ی جدول برای خروجی up به صورت زیر در میادش:
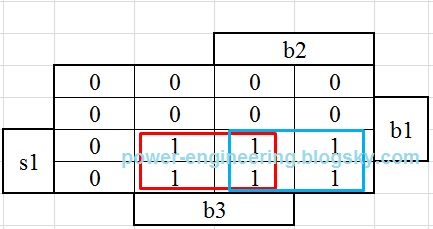
که معنی ش میشه:
up=s1.b2+s1.b3=s1.(b2+b3)
حالا فرض کنیم آسانسور در طبقه ی سوم هستش. بازهم تنها متغیرهایی که در نظر می گیریم s3 هست به همراه پوش باتونها. جدول خروجیها به صورت زیر هستش:
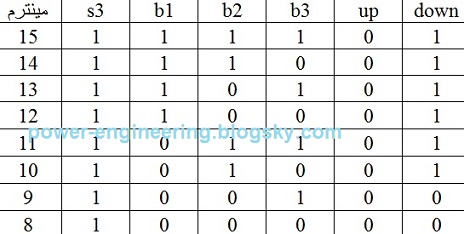
ستون خروجی up همه ی مینترماش صفره و ستون downn هر جا که b1 یا b2 (یا هر دو تاش) فشرده شده باشن برابر با یک هستش.جدول خروجی down میشه: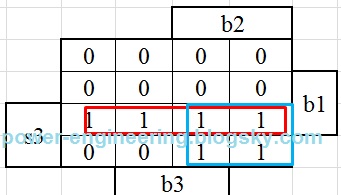
که معنی ش میشه:
down=s3.b1+s3.b2=s3.(b1+b2)
قضیه برای وقتی که آسانسور توی طبقه ی دوم ایستاده پیچیده تره. اگه آسانسور از پایین اومده باشه بالا پس upp فعال هست و باید ارزش منطقی اون رو برابر با 1 بگیریم. از طرف دیگه اگه آسانسور از طبقه ی سوم پایین اومده باشه پس downn فعال هستش و باید ارزش منطقی اون رو برابر با 1 بگیریم. از طرف دیگه می دونیم که upp و downn با همدیگه فعال نمیشن. پس به جای یه جدول بزرگ دو تا جدول کوچیک تشکیل می دیم. یه بار برای وقتی که upp=1 و دفعه ی بعدی برای وقتی که downn=1. بعد نتیجه ی حاصل رو با نتایجی که در بالا به دست آوردیم جمع می کنیم. جدول درستی خروجیها برای وقتی که upp=1 به صورت زیر هستش:
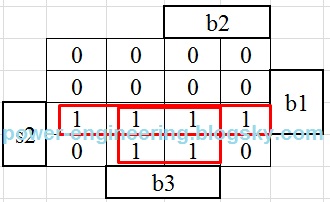
به مینترم های12ام و 14ام توجه کنید. درسته کهb1 فشرده شده اما همون طور که در قسمت دوم گفتیم در این وضعیت اتاقک آسانسور باید به حرکت خودش به سمت بالا ادامه بده و بعد برگرده پایین، پس در نتیجه خروجی upp برابر با 1شده. در نتیجه خروجی up میشه:
up=s2.upp.(b1+b3)
توجه کنید که چون فرض کردیم upp=1 باید upp رو در نتیجه ضرب بکنیم.
حالا میریم سراغ وضعیتی که downn=1 هستش:
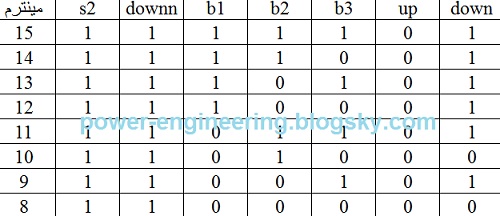
بازهم در مینترمهای 9ام و 11ام با اینکه پوش باتون b3 فشرده شده آسانسور میره پایین و علتش رو هم که در قسمت قبلی توضیح دادیم. نتیجه ی خروجی down میشه:

همون طور که می بینید این جدول با جدول خروجی up مو نمیزنه جز اینکه در اون مورد باید upp رو ضرب می کردیم و حالا باید downn رو ضرب کنیم. پس خروجی میشه:
down=s2.downn.(b1+b3)
در نهایت باید خروجی های به دست اومده از این چار تا جدول رو با هم جمع بزنیم. در نتیجه داریم:
up=(s1.(b2+b3))+(s2.upp.(b1+b3))
down=(s3.(b1+b2))+(s2.downn.(b1+b3))
یعنی دقیقا به همون نتیجه ای رسیدیم که از تحلیل مدار به دست آوردیم. اگر هم بخواهیم که این مدار رو به صورت لدر طراحی کنیم حاصل اون همون شکل اول هست. پس نتیجه می گیریم که با استفاده از ساده سازی مدار منطقی میتونیم به همون نتیجه ای برسیم که از طراحی عادی مدار فرمان به دست میادش.
اگه حوصله ای بود این بحث رو با مدار فرمان آسانسور چهار طبقه ادامه میدیم و داستان رو جمع ش می کنیم.